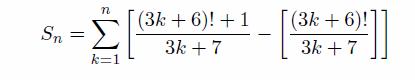HDU 2973 YAPTCHA (威尔逊定理)
YAPTCHA
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1885 Accepted Submission(s): 971
Problem Description
math department has been having problems lately. Due to immense amount
of unsolicited automated programs which were crawling across their
pages, they decided to put
Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on
their webpages. In short, to get access to their scientific papers, one
have to prove yourself eligible and worthy, i.e. solve a mathematic
riddle.
However, the test turned out difficult for some math
PhD students and even for some professors. Therefore, the math
department wants to write a helper program which solves this task (it is
not irrational, as they are going to make money on selling the
program).
The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute
where [x] denotes the largest integer not greater than x.
Input
Output
Sample Input
Sample Output
题目大意
给定一个整数n,求
题目分析
威尔逊定理:
当且仅当p为素数时,(p−1)!≡−1(mod p)
所以我们可以发现,如果这个3k+7为奇数,式子就等于1,否则就等于0
#include<bits/stdc++.h> using namespace std; const int N=;
long long a[N];
bool prime[N];
int i,n,j,x;
int main()
{
for(i=; i<N; i++)
{
if(i%==) prime[i]=false;
else prime[i]=true;
}
for(i=; i<=sqrt(N); i+=)
{
if(prime[i])
for(j=i+i; j<N; j+=i)
prime[j]=false;
}
for(i=;i<=;i++)
{
a[i]=a[i-];
if(prime[*i+])
a[i]++;
}
cin>>n;
for(i=;i<=n;i++)
{
cin>>x;
cout<<a[x]<<endl;
}
}
HDU 2973 YAPTCHA (威尔逊定理)的更多相关文章
- hdu 2973"YAPTCHA"(威尔逊定理)
传送门 题意: 给出自然数 n,计算出 Sn 的值,其中 [ x ]表示不大于 x 的最大整数. 题解: 根据威尔逊定理,如果 p 为素数,那么 (p-1)! ≡ -1(mod p),即 (p-1)! ...
- HDU - 2973 - YAPTCHA
先上题目: YAPTCHA Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)To ...
- HDU2937 YAPTCHA(威尔逊定理)
YAPTCHA Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Subm ...
- HDU - 2973:YAPTCHA (威尔逊定理)
The math department has been having problems lately. Due to immense amount of unsolicited automated ...
- hdu2973 YAPTCHA【威尔逊定理】
<题目链接> 题目大意: The task that is presented to anyone visiting the start page of the math departme ...
- HDU 5391 Zball in Tina Town【威尔逊定理】
<题目链接> Zball in Tina Town Problem Description Tina Town is a friendly place. People there care ...
- YAPTCHA UVALive - 4382(换元+威尔逊定理)
题意就是叫你求上述那个公式在不同N下的结果. 思路:很显然的将上述式子换下元另p=3k+7则有 Σ[(p-1)!+1/p-[(p-1)!/p]] 接下来用到一个威尔逊定理,如果p为素数则 ( p -1 ...
- HDU 6608:Fansblog(威尔逊定理)
Fansblog Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Subm ...
- HDU2973(威尔逊定理)
YAPTCHA Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total S ...
随机推荐
- Python 正则表达式Ⅱ
re.search方法 re.search 扫描整个字符串并返https://www.xuanhe.net/回第一个成功的匹配. 函数语法: 函数参数说明: 匹配成功re.search方法返回一个匹配 ...
- UVA 12063 Zeros and ones 一道需要好好体会的好题
#include<bits/stdc++.h> #include<stdio.h> #include<iostream> #include<cmath> ...
- 【杂题】[CodeForces 1172D] Nauuo and Portals【构造】
Description 有一个n*n的网格,你需要在上面设置一些传送门,传送门由两个配对的格子组成,从一个进入会立刻从另一个同一方向出来. 现在有n个人从第1列出发向右走,位于(i,1)的人要走到(r ...
- ubuntu搭建、安装gitlab服务器以及初始化密码
本为14.04 在搭建之前要确定其网络环境是没有问题.用root身份进行操作 1.安装和配置必要的依赖关系 apt-get update apt-get install -y curl openssh ...
- [CSP-S模拟测试]:组合(欧拉路)
题目传送门(内部题119) 输入格式 第一行,三个整数$T,M,N$. 接下来的$N$行,每行两个整数$u_i,v_i$($i$从$1$开始编号).允许$u_i=v_i$,也允许同样的简单词多次出现. ...
- Oracle提高SQL查询效率where语句条件的先后次序
(1)选择最有效率的表名顺序(只在基于规则的优化器中有效): Oracle的解析器按照从右到左的顺序处理FROM子句中的表名,FROM子句中写在最后的表(基础表 driving table)将被最先处 ...
- uswgi
1.安装uwsgi注意: 1)在系统环境安装,非虚拟环境 2)使用对应python版本安装 3)要先安装python开发包 ###sudo apt-get install python3.6-dev ...
- IDEA配置常见配置
特别提示:本人博客部分有参考网络其他博客,但均是本人亲手编写过并验证通过.如发现博客有错误,请及时提出以免误导其他人,谢谢!欢迎转载,但记得标明文章出处:http://www.cnblogs.com/ ...
- 基于Xposed hook 实时监测微信消息
本文以微信版本6.7.3为例进行分析有hook, 大部分做微信机器人的话,首先要实时抓取微信的消息,在这里展示三种方式对微信的消息进行hook: 1.基于UI层拉取加载进行监听 2.基于微信dao层调 ...
- DS博客大作业--树
1.树的存储结构说明 树节点结构体 data:文件名 brother:兄弟节点 child:孩子节点 type:节点的类型,0为文件,1为目录 h:节点所在的层次 2.树的函数说明 头文件 函数1:C ...