E. Reachability from the Capital（tarjan+dfs）

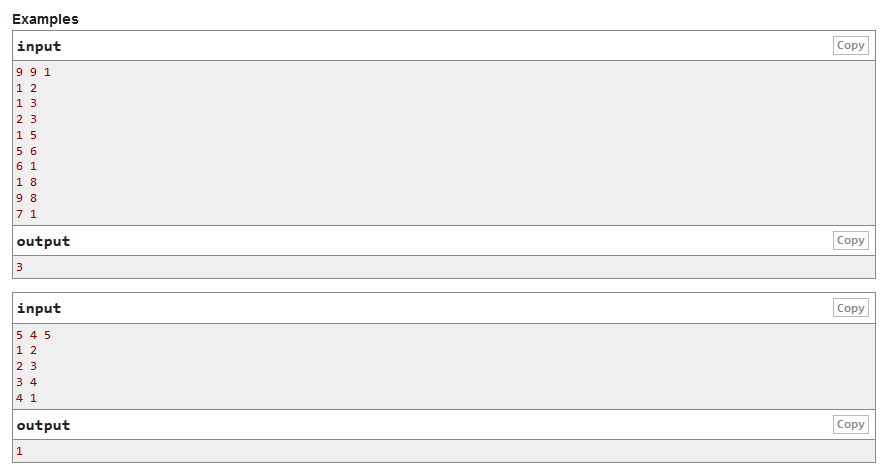
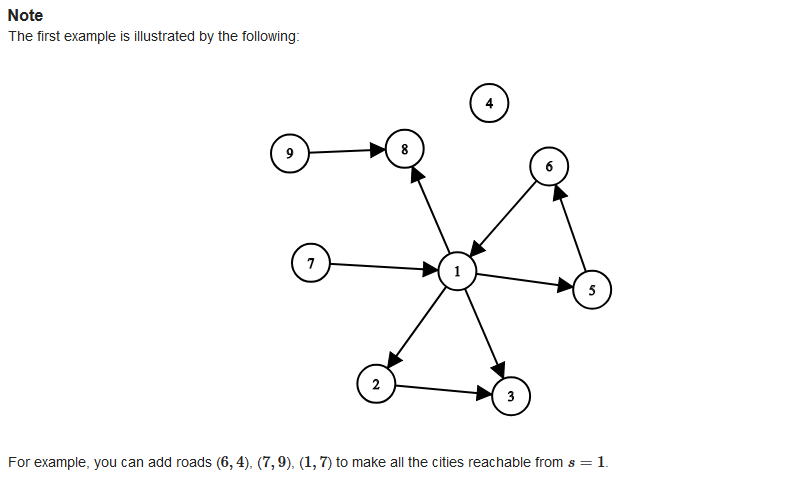
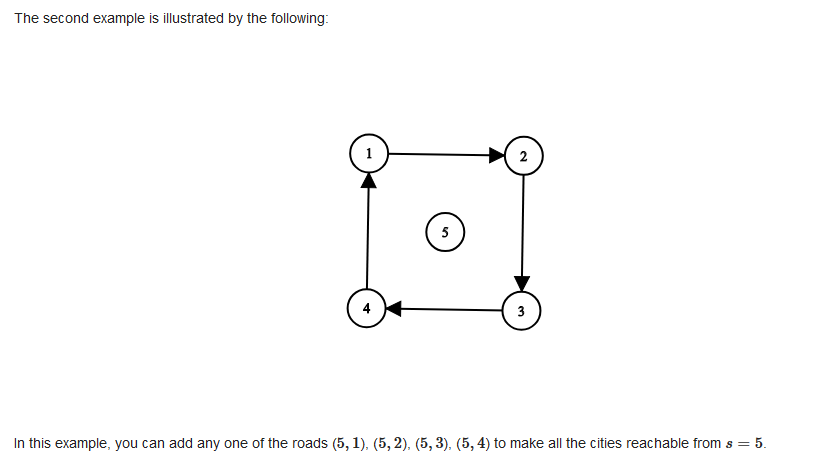
求联通分量个数，在dfs一次

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
int n,m,cap,ans=,cnt=,top=-,pos=;
int head[],low[],dnf[],Stack[],vis[];
vector<int>vv[],fv[];
int belong[],in[],u[],v[];
void tarjan(int u)
{
    low[u]=dnf[u]=++cnt;
    Stack[++top]=u;
    vis[u]=;
    int v;
    for(int i=;i<fv[u].size();i++)
    {
        v=fv[u][i];
        if(!dnf[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v]) low[u]=min(dnf[v],low[u]);
    }
    if(low[u]==dnf[u])
    {
        ans++;
        do
        {
            v=Stack[top--];
            belong[v]=ans;
            vis[v]=;
        }while(u!=v);
    }
}
void solve()
{
    memset(head,-,sizeof(head));
    memset(vis,,sizeof(vis));
    for(int i=;i<=n;i++)
        if(!dnf[i]) tarjan(i);
}
void dfs(int u)
{
    vis[u]=;
    for(int i=;i<vv[u].size();i++)
        if(!vis[vv[u][i]]) dfs(vv[u][i]);
}
int main()
{
    scanf("%d%d%d",&n,&m,&cap);
    for(int i=;i<=m;i++)
    {
        scanf("%d%d",&u[i],&v[i]);
        fv[u[i]].push_back(v[i]);
    }
    solve();
    memset(in,,sizeof(in));
    for(int i=;i<=m;i++)
    {
        if(belong[u[i]]==belong[v[i]]) continue;
        vv[belong[u[i]]].push_back(belong[v[i]]);
        in[belong[v[i]]]++;
    }
    memset(vis,,sizeof(vis));
    dfs(belong[cap]);
    int inf=;
    for(int i=;i<=ans;i++)
        inf+=(!in[i] && !vis[i]);
    printf("%d\n",inf);
    return ;
}