【十大经典数据挖掘算法】Apriori

【十大经典数据挖掘算法】系列

1. C4.5
2. K-Means
3. SVM
4. Apriori
5. EM
6. PageRank
7. AdaBoost
8. kNN
9. Naïve Bayes
10. CART

---

1. 关联分析

关联分析是一类非常有用的数据挖掘方法，能从数据中挖掘出潜在的关联关系。比如，在著名的购物篮事务（market basket transactions）问题中，

TID	Iterms
1	{Bread, Milk}
2	{Bread, Diapers, Beer, Eggs}
3	{Milk, Diapers, Beer, Cola}
4	{Bread, Milk, Diapers, Beer}
5	{Bread, Milk, Beer, Cola}

关联分析则被用来找出此类规则：顾客在买了某种商品时也会买另一种商品。在上述例子中，大部分都知道关联规则：{Diapers} → {Beer}；即顾客在买完尿布之后通常会买啤酒。后来通过调查分析，原来妻子嘱咐丈夫给孩子买尿布时，丈夫在买完尿布后通常会买自己喜欢的啤酒。但是，如何衡量这种关联规则是否靠谱呢？下面给出了度量标准。

支持度与置信度

关联规则可以描述成：项集 → 项集。项集\(X\)出现的事务次数（亦称为support count）定义为：

\[
\sigma (X) = |t_i|X \subseteq t_i, t_i \in T|
\]

其中，\(t_i\)表示某个事务（TID），\(T\)表示事务的集合。关联规则\(X \longrightarrow Y\)的支持度（support）：

\[
s(X \longrightarrow Y) = \frac{\sigma (X \cup Y)}{|T|}
\]

支持度刻画了项集\(X \cup Y\)的出现频次。置信度（confidence）定义如下：

\[
s(X \longrightarrow Y) = \frac{\sigma (X \cup Y)}{\sigma (X)}
\]

对概率论稍有了解的人，应该看出来：置信度可理解为条件概率\(p(Y|X)\)，度量在已知事务中包含了\(X\)时包含\(Y\)的概率。

对于靠谱的关联规则，其支持度与置信度均应大于设定的阈值。那么，关联分析问题即等价于：对给定的支持度阈值min_sup、置信度阈值min_conf，找出所有的满足下列条件的关联规则：

\begin{aligned}
& 支持度 >= min\_sup \cr
& 置信度 >= min\_conf \cr
\end{aligned}

把支持度大于阈值的项集称为频繁项集（frequent itemset）。因此，关联规则分析可分为下列两个步骤：

• 生成频繁项集\(F=X \cup Y\)；
• 在频繁项集\(F\)中，找出所有置信度大于最小置信度的关联规则\(X \longrightarrow Y\)。

暴力方法

若（对于所有事务集合）项的个数为\(d\)，则所有关联规则的数量：

\[
\begin{aligned}
& \sum_{i}^d C_d^i \sum_{j}^{d-i} C_{d-i}^j \cr
= & \sum_{i}^d C_d^i ( 2^{d-i} -1) \cr
= & \sum_{i}^d C_d^i * 2^{d-i} - 2^d + 1 \cr
= & (3^d - 2^d) - 2^d +1 \cr
= & 3^d - 2^{d+1} + 1
\end{aligned}
\]

如果采用暴力方法，穷举所有的关联规则，找出符合要求的规则，其时间复杂度将达到指数级。因此，我们需要找出复杂度更低的算法用于关联分析。

2. Apriori算法

Agrawal与Srikant提出Apriori算法，用于做快速的关联规则分析。

频繁项集生成

根据支持度的定义，得到如下的先验定理：

• 定理1：如果一个项集是频繁的，那么其所有的子集（subsets）也一定是频繁的。

这个比较容易证明，因为某项集的子集的支持度一定不小于该项集。

• 定理2：如果一个项集是非频繁的，那么其所有的超集（supersets）也一定是非频繁的。

定理2是上一条定理的逆反定理。根据定理2，可以对项集树进行如下剪枝：

项集树共有项集数：\(\sum_{k=1}^d k \times C_{d}^k = d \cdot 2^{d-1}\)。显然，用穷举的办法会导致计算复杂度太高。对于大小为\(k-1\)的频繁项集\(F_{k-1}\)，如何计算大小为\(k\)的频繁项集\(F_k\)呢？Apriori算法给出了两种策略：

1. \(F_k = F_{k-1} \times F_1\)方法。之所以没有选择\(F_{k-1}\)与（所有）1项集生成\(F_k\)，是因为为了满足定理2。下图给出由频繁项集\(F_2\)与\(F_1\)生成候选项集\(C_3\)：
   

2. \(F_k = F_{k-1} \times F_{k-1}\)方法。选择前\(k-2\)项均相同的\(f_{k-1}\)进行合并，生成\(F_{k-1}\)。当然，\(F_{k-1}\)的所有\(f_{k-1}\)都是有序排列的。之所以要求前\(k-2\)项均相同，是因为为了确保\(F_k\)的\(k-2\)项都是频繁的。下图给出由两个频繁项集\(F_2\)生成候选项集\(C_3\)：
   

生成频繁项集\(F_k\)的算法如下：

关联规则生成

关联规则是由频繁项集生成的，即对于\(F_k\)，找出项集\(h_m\)，使得规则\(f_k-h_m \longrightarrow h_m\)的置信度大于置信度阈值。同样地，根据置信度定义得到如下定理：

定理3：如果规则\(X \longrightarrow Y-X\)不满足置信度阈值，则对于\(X\)的子集\(X'\)，规则\(X' \longrightarrow Y-X'\)也不满足置信度阈值。

根据定理3，可对规则树进行如下剪枝：

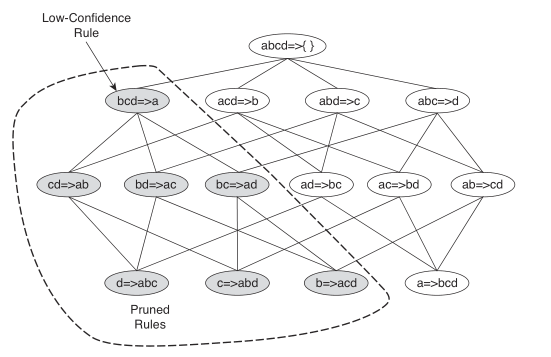
关联规则的生成算法如下：

3. 参考资料

[1] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.