图数据库PageRank算法

目录：

• 定义
• 计算原理

定义：

假设对象A具有指向它的对象T₁ ... T_n。参数d是阻尼系数，取值范围在0和1之间，通常将d设置为0.85。C（A）被定义为从对象A出去的连接数。

对象A的PageRank计算公式如下：

PR（A）=（−d）+d（PR（T1）/C（T1）+...+PR（Tn）/C（Tn））

当一个节点只有输出，没有输入的时候，因为d一般设置为0.85，所以：

PR（A）=（-d）+ d *（）= 0.15

计算原理：

每个对象的PR取决于指向它的对象的PR。在指向一个对象的所有对象都计算出了PR，才能够计算出该页面的PR值。

当所有对象形成闭环时，PR（A）可以使用简单的迭代算法计算，并且对应于web的规范化链接矩阵的主特征向量。

基本上，每次计算都会对各对象的最终值进行更接近的估计。通过对这些对象进行大量重复的计算，直到结果变化很小为止。

示例1：

每个页面都有一个输出链接（输出计数为1，即C（A）= 1，C（B）= 1）

假设A的PR（A）初始值为1

d = 0.85          //默认值
 
PR（A）=（ - d）+ d（PR（B）/ ）
 
PR（B）=（ - d）+ d（PR（A）/ ）
 
//即
 
PR（A）= 0.15 + 0.85 *  = 
 
PR（B）= 0.15 + 0.85 *  = 

假设A的PR（A）初始值为0

PR（A）= 0.15 + 0.85 *  = 0.15
 
PR（B）= 0.15 + 0.85 * 0.15 = 0.2775
 
//完成一次迭代，继续第二次迭代
 
PR（A）= 0.15 + 0.85 * 0.2775 = 0.385875
 
PR（B）= 0.15 + 0.85 * 0.385875 = 0.47799375
 
//第三次迭代
 
PR（A）= 0.15 + 0.85 * 0.47799375 = 0.5562946875
 
PR（B）= 0.15 + 0.85 * 0.5562946875 = 0.622850484375
 
//结果数值不断上升，但当达到1.0时，停止增加。

假设A的PR（A）初始值为40，B的PR（B）初始值为40

//初始值
PR（A）=
PR（B）= 
 
//第一次迭代
 
PR（A）= 0.15 + 0.85 *  = 34.25
 
PR（B）= 0.15 + 0.85 * 0.385875 = 29.1775
 
//第二次迭代
 
PR（A）= 0.15 + 0.85 * 29.1775 = 24.950875
 
PR（B）= 0.15 + 0.85 * 24.950875 = 21.35824375
 
//结果数值不断下降，但当达到1.0时，停止下降。

性质：

当没有节点只进不出时，PageRank计算结果符合“ 归一化概率分布 ”，所有节点的PageRank平均值为1.0。

示例2：

该实例不满足只进不出条件，第三列的节点只有输入，没有输出，所以PR的平均值不等于1.0

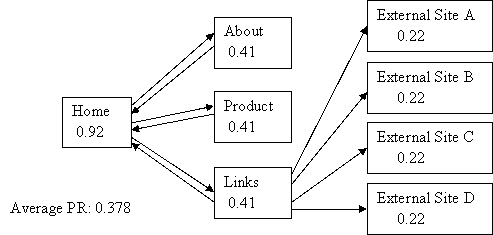
参考资料：

http://www.cs.princeton.edu/~chazelle/courses/BIB/pagerank.htm