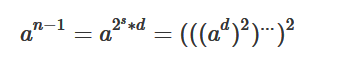大素数测试的Miller-Rabin算法
Miller-Rabin算法本质上是一种概率算法,存在误判的可能性,但是出错的概率非常小。出错的概率到底是多少,存在严格的理论推导。
一、费马小定理
假如p是质数,且gcd(a,p)=1,那么 a(p-1)≡1(mod p)
如果存在a<p,且a(p-1) % p != 1,则p肯定不是素数。
二、有限域上的平方根定理
三、Miller-Rabin算法
对于一个大数n,判断n是不是素数的时候,可以先考虑a(n-1)≡ 1(mod n)
对于n-1,一定可以拆分成2s+d:
可以从x = ad开始,依次平方s次,每次平方的时候模上n,按照之前的平方根定理,如果模上n的结果为1的话,那么x一定是1,或者是n-1,如果不满足则不是素数,x=x2,再次循环。
每次随机选一个在2-n-1的数字作为a,可以重复测试。
由于mod上的是n,n是一个大数,所以快速幂中的乘法,需要用快速加法来实现。不然就算模上之后再相乘也会溢出。
#include<iostream>
#include<ctime>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = +;
ll mul(ll a, ll b, ll m)
//求a*b%m
{
ll ans = ;
a %= m;
while(b)
{
if(b & )ans = (ans + a) % m;
b /= ;
a = (a + a) % m;
}
return ans;
}
ll pow(ll a, ll b, ll m)
//a^b % m
{
ll ans = ;
a %= m;
while(b)
{
if(b & )ans = mul(a, ans, m);
b /= ;
a = mul(a, a, m);
}
ans %= m;
return ans;
}
bool Miller_Rabin(ll n, int repeat)//n是测试的大数,repeat是测试重复次数
{
if(n == || n == )return true;//特判
if(n % == || n == )return false;//偶数和1 //将n-1分解成2^s*d
ll d = n - ;
int s = ;
while(!(d & )) ++s, d >>= ;
srand((unsigned)time(NULL));
for(int i = ; i < repeat; i++)//重复repeat次
{
ll a = rand() % (n - ) + ;//取一个随机数,[2,n-1)
ll x = pow(a, d, n);
ll y = ;
for(int j = ; j < s; j++)
{
y = mul(x, x, n);
if(y == && x != && x != (n - ))return false;
x = y;
}
if(y != )return false;//费马小定理
}
return true;
}
int main()
{
int T;
cin >> T;
ll n;
while(T--)
{
cin >> n;
if(Miller_Rabin(n, ))cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
大素数测试的Miller-Rabin算法的更多相关文章
- 【数论基础】素数判定和Miller Rabin算法
判断正整数p是否是素数 方法一 朴素的判定
- Miller Rabin算法详解
何为Miller Rabin算法 首先看一下度娘的解释(如果你懒得读直接跳过就可以反正也没啥乱用:joy:) Miller-Rabin算法是目前主流的基于概率的素数测试算法,在构建密码安全体系中占有重 ...
- Miller Rabin算法学习笔记
定义: Miller Rabin算法是一个随机化素数测试算法,作用是判断一个数是否是素数,且只要你脸不黑以及常数不要巨大一般来讲都比\(O(\sqrt n)\)的朴素做法更快. 定理: Miller ...
- Miller Rabin 算法简介
0.1 一些闲话 最近一次更新是在2019年11月12日.之前的文章有很多问题:当我把我的代码交到LOJ上,发现只有60多分.我调了一个晚上,尝试用{2, 3, 5, 7, 11, 13, 17, 1 ...
- Miller_Rabbin大素数测试
伪素数: 如果存在和n互素的正整数a满足a^(n-1)≡1(mod n),则n是基于a的伪素数. 是伪素数但不是素数的个数是非常非常少的,所以如果一个数是伪素数,那么他几乎是素数. Miller_Ra ...
- Pollard rho算法+Miller Rabin算法 BZOJ 3668 Rabin-Miller算法
BZOJ 3667: Rabin-Miller算法 Time Limit: 60 Sec Memory Limit: 512 MBSubmit: 1044 Solved: 322[Submit][ ...
- 关于素数:求不超过n的素数,素数的判定(Miller Rabin 测试)
关于素数的基本介绍请参考百度百科here和维基百科here的介绍 首先介绍几条关于素数的基本定理: 定理1:如果n不是素数,则n至少有一个( 1, sqrt(n) ]范围内的的因子 定理2:如果n不是 ...
- (Miller Rabin算法)判断一个数是否为素数
1.约定 x%y为x取模y,即x除以y所得的余数,当x<y时,x%y=x,所有取模的运算对象都为整数. x^y表示x的y次方.乘方运算的优先级高于乘除和取模,加减的优先级最低. 见到x^y/z这 ...
- 米勒罗宾素性测试(Miller–Rabin primality test)
如何判断一个素是素数 效率很高的筛法 打个表 (素数的倍数一定是合数) 就可以解决问题. 筛选法的效率很高,但是遇到大素数就无能为力了. 米勒罗宾素性测试是一个相当著名的判断是否是素数的算法 核心为费 ...
- Miller-Rabin大素数测试模板
根据费马小定理: 对于素数n,a(0<a<n),a^(n-1)=1(mod n) 如果对于一个<n的正整数a,a^(n-1)!=1(mod n),则n必不是素数. 然后就可以随机生成 ...
随机推荐
- 44个 Javascript 变态题解析
原题来自: http://javascript-puzzlers.herokuapp.com/ 读者可以先去做一下感受感受. 当初笔者的成绩是 21/44... 当初笔者做这套题的时候不仅怀疑智商, ...
- IT自由职业者的第一个月(上)——何去何从
2016年8月11号,我终于走完所有流程,拿到了离职证明,5年的嵌入式驱动开发工程师的职业生涯就此结束.走离职流程期间,陆续有同事和朋友问我,离职后去哪儿,我都是告诉他们:“还没想好,离了再 ...
- Laravel 使用Voyager导致多个数据库连接总是返回默认连接?
问题与分析 最近的项目碰到一个奇怪的问题,在Laravel(5.3)中想建立多个数据库连接连到MySQL的不同数据库(另一个连接名为conn2),执行如下语句得到却发现得到的仍然是默认连接: $con ...
- 图像的点运算----底层代码与Halcon库函数
最基本的图像分析工具----灰度直方图.使用直方图辅助,可以实现4大灰度变换,包括线性灰度变换(灰度拉伸).灰度对数变换.灰度伽马变换.灰度分段线性变换:使用直方图修正技术,可以实现2大变换,包括直方 ...
- Nuxt.js学习心得
一.官网 Nuxt.js - Universal Vue.js Applications https://nuxtjs.org/ 二.中文官网 Nuxt.js - Vue.js 通用应用框架 http ...
- Angular4 step by step.1
1.官网地址 :https://angular.cn/guide/quickstart 2.在线学习地址:https://embed.plnkr.co/?show=preview 3.效果截图哇哈哈
- spring AOP Capability and Goals(面向方面编程功能和目标归纳)
原官方文档链接: https://docs.spring.io/spring/docs/5.1.6.RELEASE/spring-framework-reference/core.html#aop-i ...
- Hadoop 完全分布式部署(三节点)
用来测试,我在VMware下用Centos7搭起一个三节点的Hadoop完全分布式集群.其中NameNode和DataNode在同一台机器上,如果有条件建议大家把NameNode单独放在一台机器上,因 ...
- flight学习笔记
Flight::db()-> getOne("select 1"); 返回结果:1 Flight::db()-> getRow ("select 1, 2 f ...
- Effective C++ .09 不在构造和析构过程中调用virtual函数
看过C++对象模型的话就可以知道,在构造基类时,完整的vtable没有建立起来(表项没有被相应的子类函数替换),因而无法调用到子类的函数(即构造函数中的virtual函数是本类里的方法,不是virtu ...