Gradient descend 梯度下降法和归一化、python中的实现（未完善）

梯度下降法

　　通常就是将一组输入样本的特征$x^i$传入目标函数中，如$f(x) = wx + b$，再计算每个样本通过函数预测的值$f(x^i)$与其真实值（标签）$y^i$之差，然后计算所有差的平方和获得一个关于$w$损失函数$L(w)$：

$L(w) = \sum\limits_{i=0}^m [f(x^i) - y^i]^2 =  \sum\limits_{i=0}^m (wx^i + b - y^i)^2 $

　　目标就是让通过调整$w$让这个损失函数尽量小。首先给$w$一个随机的初始值，然后每次朝着梯度的反方向更新一下$w$的位置，这样就能使损失函数达到一个局部最小点$w^*$。

$w^{t+1} = w^t - \eta\Delta L(w^t)$

梯度下降法常用方法

　　对于$\eta$的选取要灵活，因为如果过大，迭代可能会跳过了极小点，过小又导致迭代过慢。通常是让$\eta$刚开始大一些，随着迭代逐渐减小。如：

$\eta^{t} = \frac{\eta}{\sqrt{t+1}}$， $t$从$0$开始

Adagrad

　　为了平衡每次迭代函数下降的大小，Adagrad 方法在学习速率$\eta^t$下面再除以了一项$\sigma^t$:

$\eta^t = \eta^t / \sigma^t$

$\sigma^t = \sqrt{\sum\limits_{i=0}^t (g^i)^2/(t+1)}, g^i = \Delta L(w^i) $

　　$\sqrt{t+1}$与上面抵消掉得：

$\eta^{t} = \frac{\eta}{\sum\limits_{i=0}^t (g^i)^2}$

　　则$w^{t+1}$为：

$w^{t+1} = w^t - \frac{\eta}{\sqrt{\sum\limits_{i=0}^t (g^i)^2}}\Delta L(w^t)$

　　以下是用Adagrad实现的梯度下降python代码：

import numpy as np
import matplotlib.pyplot as plt
import pandas

#x和y的数据集
x_data = np.array([338., 333., 328., 207., 226., 25., 179., 60., 208., 606.])
y_data = np.array([640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.])

#设置下降参数w和b将要画的等高线图的范围
x_b = np.arange(-200,-100,1)
y_w = np.arange(-5,5,0.1)
X,Y = np.meshgrid(x_b,y_w)
#设置w、b参数网格并给所有网格点计算相应的损失函数（用于画损失函数的等高线图 ）
Z_loss = np.zeros([len(x_b),len(y_w)])
for i in range(len(x_b)):
    for j in range(len(y_w)):
        w = y_w[j]
        b = x_b[i]
        for n in range(len(x_data)):
            Z_loss[j][i] += (y_data[n] - x_data[n] * w - b) ** 2
#梯度下降迭代次数
itera_time = 100000
#初始化w和b
w = -4.
b = -120.
#初始化列表，存w和b的迭代经过，用于画图
w_history = [w]
b_history = [b]
#设置Adagrad学习率的上半部分
lr = 1
#初始化Adagrad学习率的下半部分
lr_b = 0.
lr_w = 0.
#进行梯度下降
for i in range(itera_time):
    #每次迭代计算梯度
    b_grad = 0.;
    w_grad = 0.;
    for n in range(len(x_data)):
        b_grad += -2. * (y_data[n] - w*x_data[n] - b)
        w_grad += -2. * (y_data[n] - w*x_data[n] - b) * x_data[n]
    #给Adagrad学习率的下半部分加上每次迭代的梯度平方
    lr_b += b_grad**2
    lr_w += w_grad**2
    #w和b改变一次位置
    w -= w_grad * lr / np.sqrt(lr_w)
    b -= b_grad * lr / np.sqrt(lr_b)
    #存入这次迭代
    w_history.append(w);
    b_history.append(b);
#画等高线图
plt.contourf(X,Y,Z_loss,alpha=0.5,levels=50,cmap = 'jet')
#标出最优解
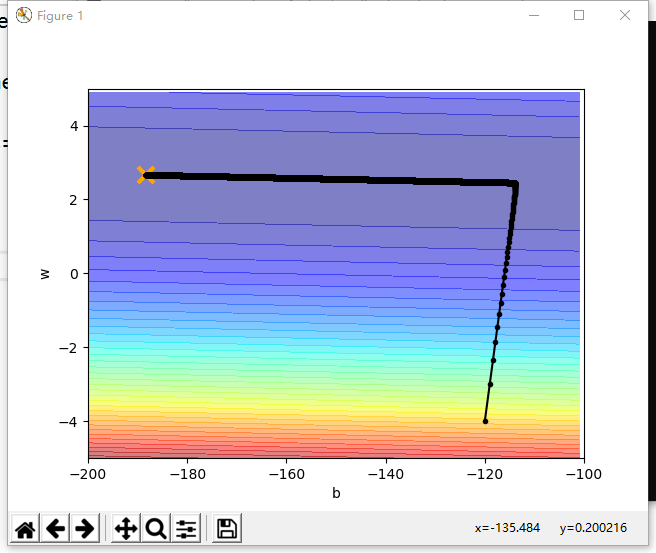
plt.plot([-188.4],[2.67],'x',ms=12,mew=3,color='orange')
#画出迭代经过
plt.plot(b_history,w_history,'o-',ms=3,lw=1.5,color='black')
#设置图像x、y轴显示宽度
plt.ylim(-5,5)
plt.xlim(-200,-100)
plt.ylabel("w")
plt.xlabel("b")
plt.show()

　　以下是代码的运行结果图，可以看到参数w和b最终迭代到了最优点：

归一化

　　还有重要的一点是，最好在开始迭代之前，先把输入的各个参数的分布进行归一化（Feature scaling）。

　　比如输入样本有两个元素$x1$和$x2$，它们的分布如下图：

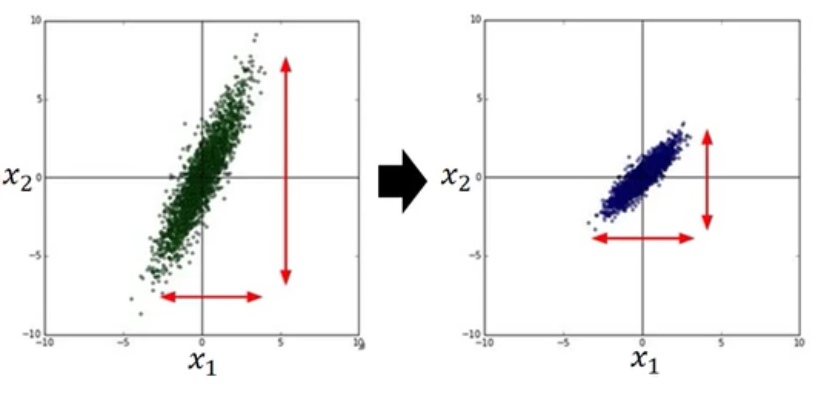
　　当梯度下降法进行的时候，它们迭代的路径就会有如下差别（因为是线性相乘的$wx$，所以$x2$的分布宽导致了$w2$方向的函数更加窄）：

　　可以明显看到，归一化后的迭代会更平滑，更直接，没归一化的迭代会随着等高线扭曲前进，增加迭代次数。

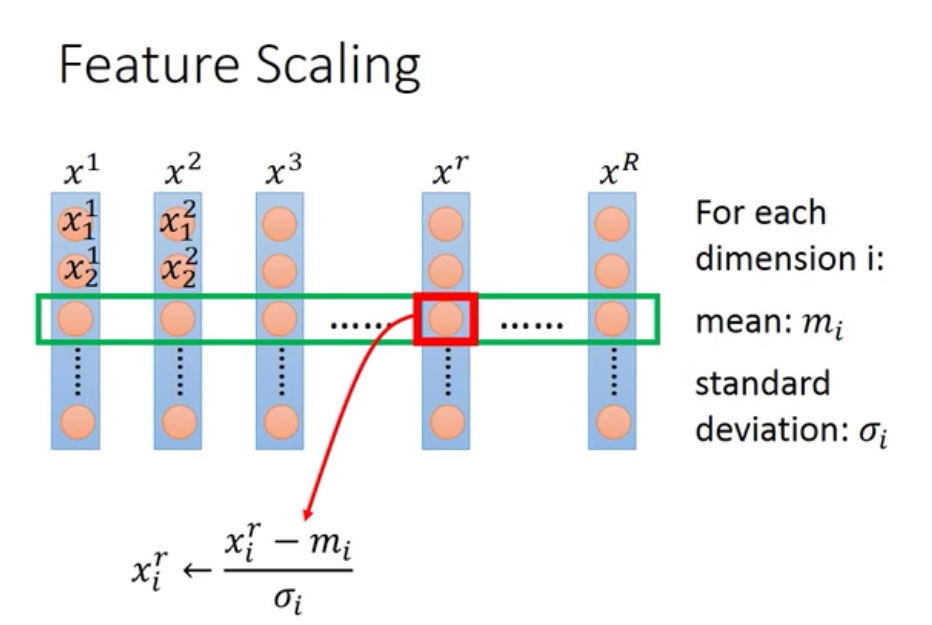
　　归一化的方法就是对于输入的每一个维度都单独计算它们的平均值和标准差，然后把每个元素都减去均值后再除以标准差：

　　那么归一化后的样本传入函数以后，优化完毕的参数还需要反归一化，具体怎么做呢？

。。。。。。