.NET实现堆排序

堆排序及相关知识

堆排序

　　堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

堆

　　堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

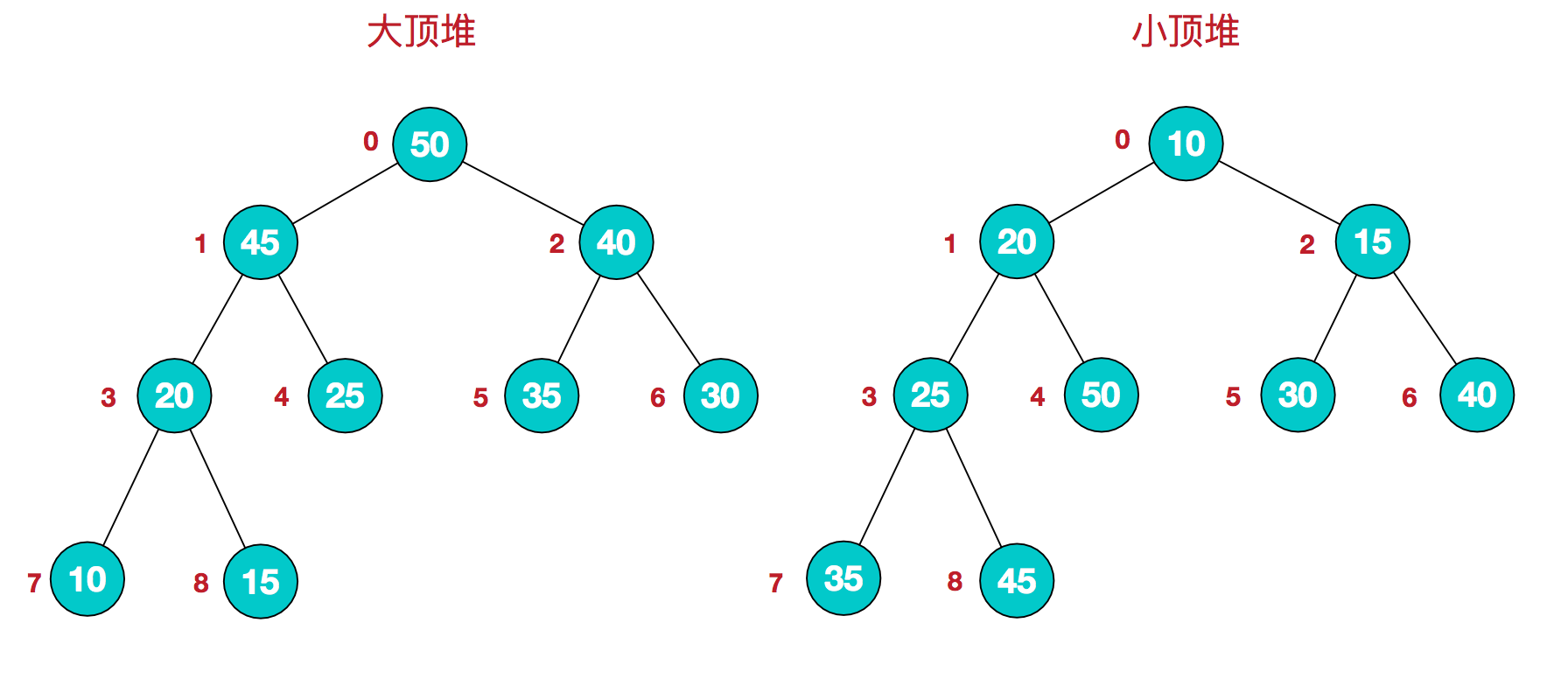
同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

ok，了解了这些定义。接下来，我们来看看堆排序的基本思想及基本步骤：

堆排序基本思想及步骤

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

　题目：假设给定无序序列结构如下

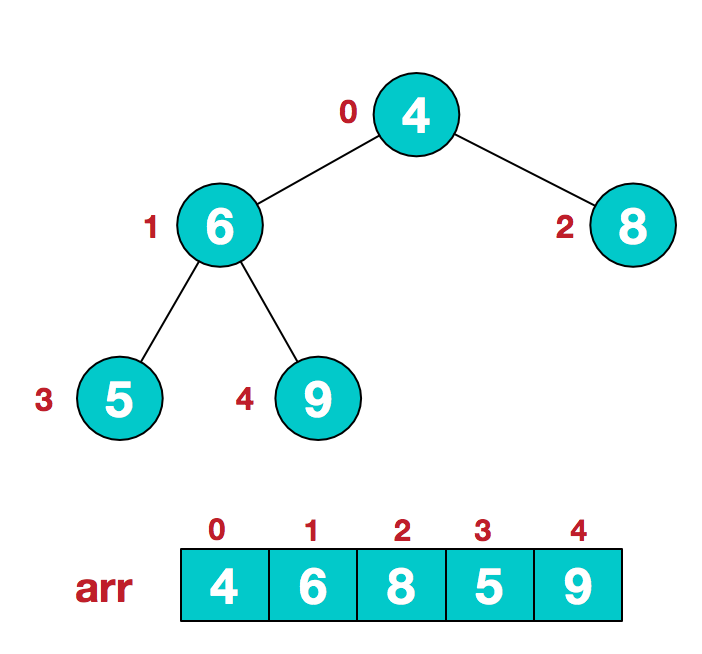
1. 此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

1. 找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

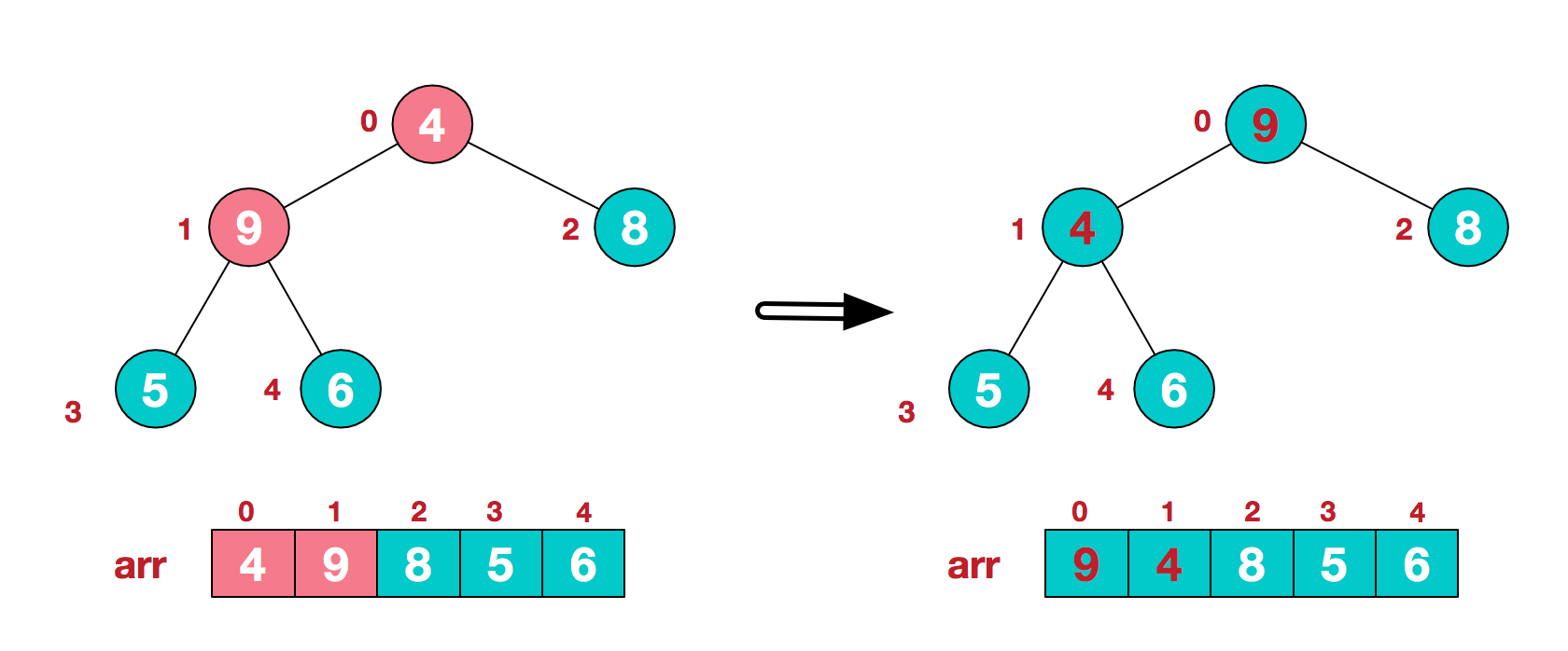
这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

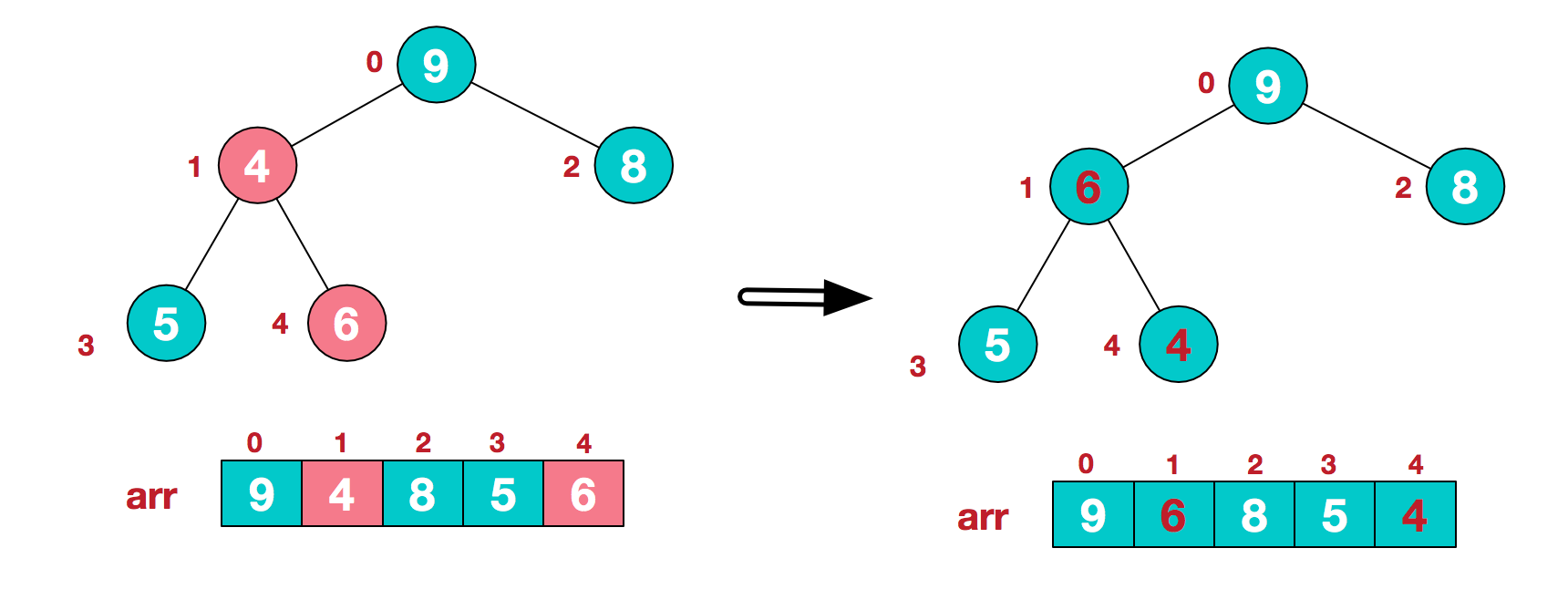
此时，我们就将一个无需序列构造成了一个大顶堆。

步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

a. 将堆顶元素9和末尾元素4进行交换

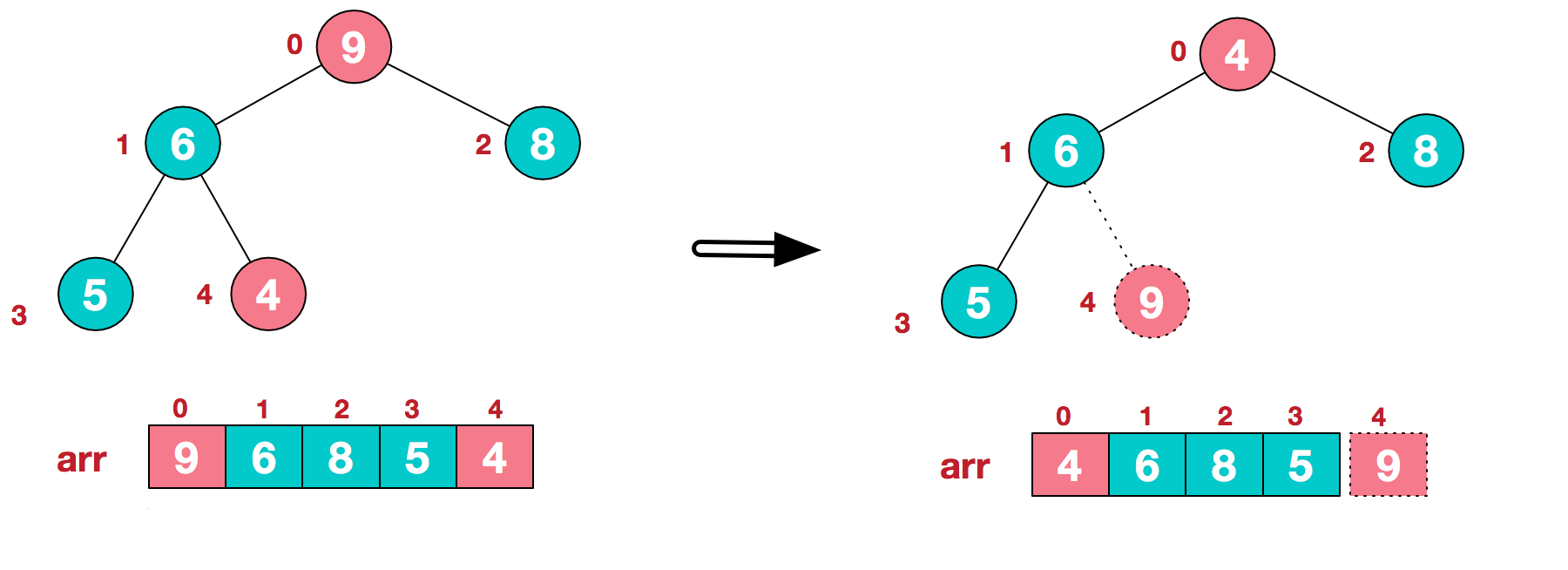
b. 重新调整结构，使其继续满足堆定义

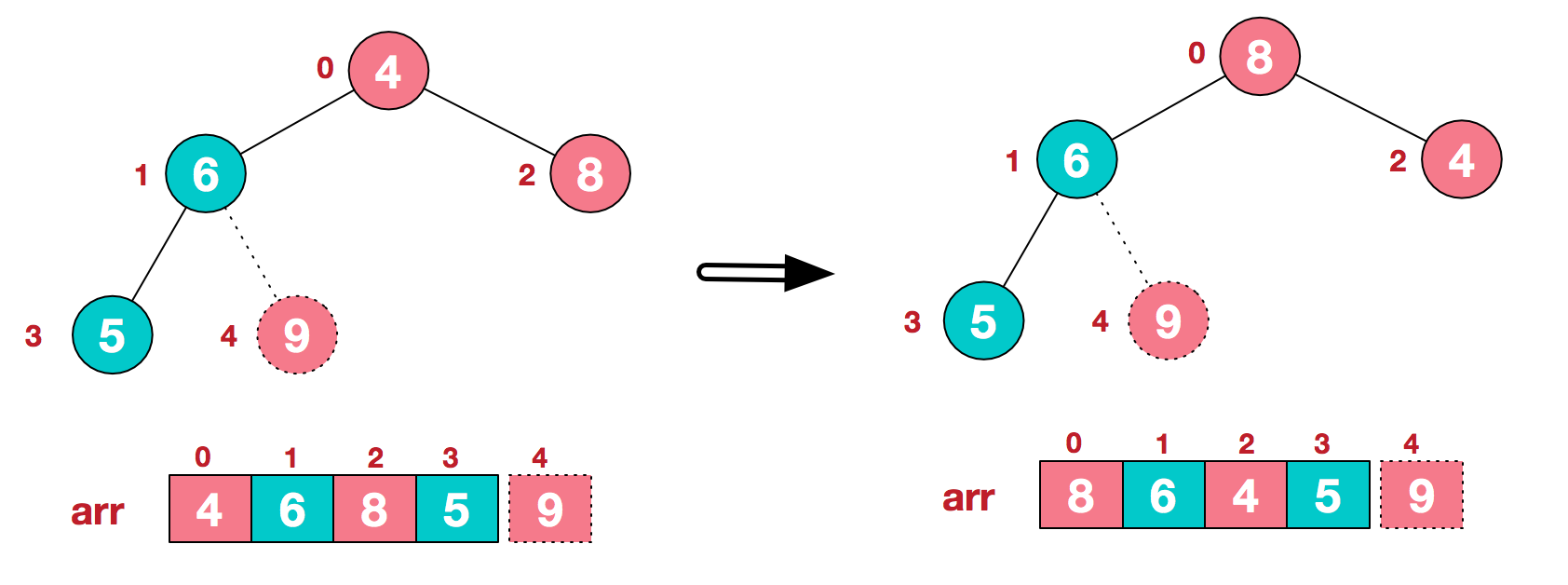
c. 再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

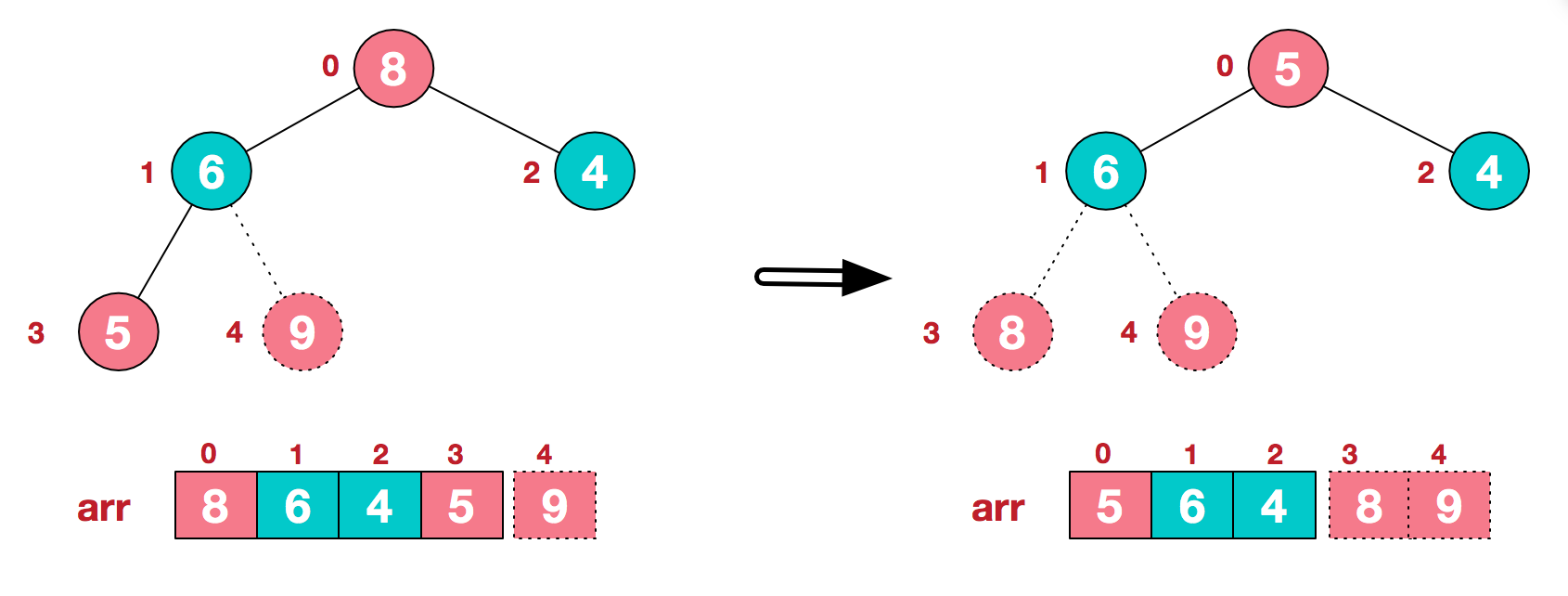
后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

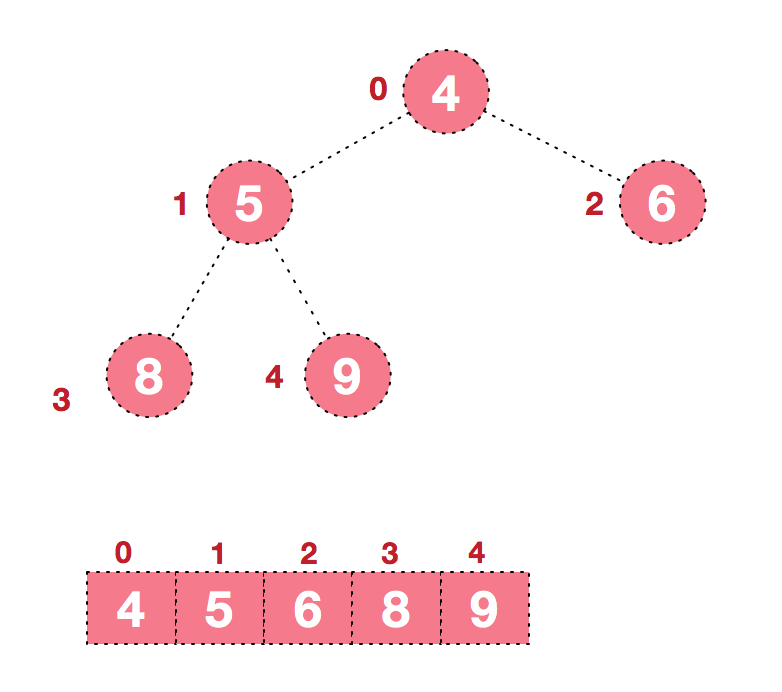
再简单总结下堆排序的基本思路：

　　a. 将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b. 将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c. 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

.NET代码实现

//对于大顶堆：arr[i] >= arr[2i + 1] && arr[i] >= arr[2i + 2]
//对于小顶堆：arr[i] <= arr[2i + 1] && arr[i] <= arr[2i + 2]
//1、将无序序列构建成一个大顶堆。
//2.将堆顶元素和最后一个元素交换，然后将剩下的节点重新构造成一个大顶堆；
//3.重复步骤2，如此反复，从第一次构建大顶堆开始，每一次构建，我们都能获得一个序列的最大值，然后把它放到大顶堆的尾部。最后，就得到一个有序的序列了

//3, 2, 3, 1, 2, 4, 5, 5, 6
public int[] HeapSort(int[] nums)
{
  //1.构建初始堆

  //这里元素的索引是从0开始的,所以最后一个非叶子结点array.length/2 - 1
  for (int i = nums.Length / 2 - 1; i >= 0; i--)
  {
    adjustHeap(nums, i, nums.Length);
  }
  // 上述逻辑，建堆结束
  //2.下面，开始排序逻辑
  for (int j = nums.Length - 1; j > 0; j--)
  {
    // 元素交换,作用是去掉大顶堆
    // 把大顶堆的根元素，放到数组的最后；换句话说，就是每一次的堆调整之后，都会有一个元素到达自己的最终位置
    swap(nums, 0, j);
    // 元素交换之后，毫无疑问，最后一个元素无需再考虑排序问题了。
    // 接下来我们需要排序的，就是已经去掉了部分元素的堆了，这也是为什么此方法放在循环里的原因
    // 而这里，实质上是自上而下，自左向右进行调整的
    adjustHeap(nums, 0, j);
  }
  return nums;
}
public static void adjustHeap(int[] array, int i, int length)
{
  // 先把当前元素取出来，因为当前元素可能要一直移动
  int temp = array[i];
  for (int k = 2 * i + 1; k < length; k = 2 * k + 1)
  {  //2*i+1为左子树i的左子树(因为i是从0开始的),2*k+1为k的左子树
   // 让k先指向子节点中最大的节点
    if (k + 1 < length && array[k] < array[k + 1])
    {  //如果有右子树,并且右子树大于左子树
        k++;
    }
    //如果发现结点(左右子结点)大于根结点，则进行值的交换
    if (array[k] > temp)
    {
        swap(array, i, k);
        // 如果子节点更换了，那么，以子节点为根的子树会受到影响,所以，循环对子节点所在的树继续进行判断
        i = k;
    }
    else
    {  //不用交换，直接终止循环
        break;
    }
}
}
public static void swap(int[] arr, int a, int b)
{
  int temp = arr[a];
  arr[a] = arr[b];
  arr[b] = temp;
}

.NET中堆排序源码

 private void Heapsort(int lo, int hi)
 {
  int n = hi - lo + 1;
  for (int i = n / 2; i >= 1; i--)
  {
      DownHeap(i, n, lo);
  }
  for (int i = n; i > 1; i--)
  {
      Swap(lo, lo + i - 1);

      DownHeap(1, i - 1, lo);
  }
}

private void DownHeap(int i, int n, int lo)
{
  object? d = keys.GetValue(lo + i - 1);
  object? dt = items?.GetValue(lo + i - 1);
  int child;
  while (i <= n / 2)
  {
      child = 2 * i;
      if (child < n && comparer.Compare(keys.GetValue(lo + child - 1), keys.GetValue(lo + child)) < 0)
      {
          child++;
      }

      if (!(comparer.Compare(d, keys.GetValue(lo + child - 1)) < 0))
          break;

      keys.SetValue(keys.GetValue(lo + child - 1), lo + i - 1);
      items?.SetValue(items.GetValue(lo + child - 1), lo + i - 1);
      i = child;
  }
  keys.SetValue(d, lo + i - 1);
  items?.SetValue(dt, lo + i - 1);
}

感谢博主：https://www.cnblogs.com/chengxiao/p/6129630.html