HDU 1198 Farm Irrigation （并检查集合 和 dfs两种实现）

Farm Irrigation

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 4977    Accepted Submission(s): 2137

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A
to K, as Figure 1 shows.






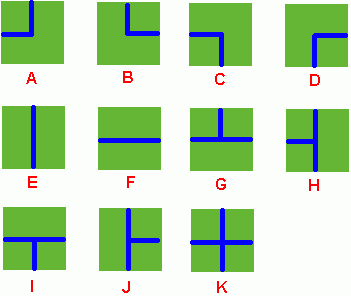
Figure 1




Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map 



ADC

FJK

IHE



then the water pipes are distributed like 






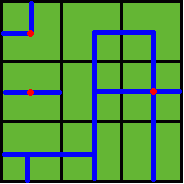
Figure 2




Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn. 



Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative
M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

Sample Input

2 2
DK
HF

3 3
ADC
FJK
IHE

-1 -1

 

Sample Output

2
3

 

题意：有如上图11种土地块，块中的绿色线条为土地块中修好的水渠，如今一片土地由上述的各种土地块组成，须要浇水，问须要打多少口井。

比如以下这个土地块

ADC

FJK

IHE



then the water pipes are distributed like

如图对于能相连的地仅仅须要打一口井。所以以上须要打三口井就能浇全部的块。稍加分析就可得出本质上就是集合的合并，最后求有几个集合的问题，非常easy想到并查集。仅仅须要对每一个地块与右方和下方的地块进行合并就可以。

合并之前先推断能否连通。若能连通则合并。不能连通，则不能合并。

能连通的时候就是正常的并查集了。此题有个问题，题目说最大50*50个地块，可是提交一直出错，看别人说的改成550*550直接A了，所以说这里题目叙述有误。
后来想了想。能够把每一个地块的四个方向用二进制来表示，用位运算来推断可连性。

#include <cstdio>
#include <cstdlib>
#include <climits>

const int MAX = 550;

//存储11中类型的土地，二维中的0 1 2 3分别代表这样的类型的土地的左上右下
//为1表示这个方向有接口。为0表示这个方向没有接口
const int type[11][4]={{1,1,0,0},{0,1,1,0},
						{1,0,0,1},{0,0,1,1},
						{0,1,0,1},{1,0,1,0},
						{1,1,1,0},{1,1,0,1},
						{1,0,1,1},{0,1,1,1},
						{1,1,1,1}
						};

const bool VERTICAL = true;

//pre数组就是正常的并查集中所用，可是在合并的时候要注意将二维坐标转换成一维的标号，此处用行优先
int pre[MAX*MAX+1],cnt,m,n;
char farm[MAX][MAX];

void init(int n){
	int i;
	for(i=1;i<=n;++i){
		pre[i] = i;
	}
	cnt = n;
}

int root(int x){
	if(x!=pre[x]){
		pre[x] = root(pre[x]);
	}
	return pre[x];
}

void merge(int ax,int ay,int bx,int by,bool dir){
	if(bx>n || by>m)return;//超出地图的部分不进行合并
	bool mark = false;//标识两块地是否可连
	int ta,tb;//两点的类型值0-10

	ta = farm[ax][ay]-'A';
	tb = farm[bx][by]-'A';

	if(dir){//竖直方向推断可连性
		if(type[ta][3] && type[tb][1])mark = true;
	}else{//水平方向推断可连性
		if(type[ta][2] && type[tb][0])mark = true;
	}

	if(mark){//仅仅要可连就合并，这就是正常的并查集了
		int fx = root((ax-1)*m+ay);
		int fy = root((bx-1)*m+by);
		if(fx!=fy){
			pre[fy] = fx;
			--cnt;
		}
	}
}

int main(){
	//freopen("in.txt","r",stdin);
	int i,j;
	while(scanf("%d %d",&n,&m)!=EOF){
		if(n==-1 && m==-1)break;
		init(n*m);
		for(i=1;i<=n;++i){
			scanf("%s",farm[i]+1);
		}
		for(i=1;i<=n;++i){
			for(j=1;j<=m;++j){
				merge(i,j,i+1,j,VERTICAL);
				merge(i,j,i,j+1,!VERTICAL);
			}
		}
		printf("%d\n",cnt);
	}
	return 0;
}

下面是位运算的实现，就相对简化了点。

#include <cstdio>
#include <cstdlib>
#include <climits>

const int MAX = 550;

const int type[11] = {3,6,9,12,10,5,7,11,13,14,15};
const bool VERTICAL = true;

//pre数组就是正常的并查集中所用，可是在合并的时候要注意将二维坐标转换成一维的标号。此处用行优先
int pre[MAX*MAX+1],cnt,m,n;
char farm[MAX][MAX];

void init(int n){
	int i;
	for(i=1;i<=n;++i){
		pre[i] = i;
	}
	cnt = n;
}

int root(int x){
	if(x!=pre[x]){
		pre[x] = root(pre[x]);
	}
	return pre[x];
}

void merge(int ax,int ay,int bx,int by,bool dir){
	if(bx>n || by>m)return;//超出地图的部分不进行合并
	bool mark = false;//标识两块地是否可连
	int ta,tb;//两点的类型值0-10

	ta = farm[ax][ay]-'A';
	tb = farm[bx][by]-'A';

	if(dir){//竖直方向推断可连性
		if(((type[ta]>>3) & 1) && ((type[tb]>>1) & 1))mark = true;
	}else{//水平方向推断可连性
		if(((type[ta]>>2) & 1) && (type[tb] & 1))mark = true;
	}

	if(mark){//仅仅要可连就合并，这就是正常的并查集了
		int fx = root((ax-1)*m+ay);
		int fy = root((bx-1)*m+by);
		if(fx!=fy){
			pre[fy] = fx;
			--cnt;
		}
	}
}

int main(){
	//freopen("in.txt","r",stdin);
	int i,j;
	while(scanf("%d %d",&n,&m)!=EOF){
		if(n==-1 && m==-1)break;
		init(n*m);
		for(i=1;i<=n;++i){
			scanf("%s",farm[i]+1);
		}
		for(i=1;i<=n;++i){
			for(j=1;j<=m;++j){
				merge(i,j,i+1,j,VERTICAL);
				merge(i,j,i,j+1,!VERTICAL);
			}
		}
		printf("%d\n",cnt);
	}
	return 0;
}

下面是dfs实现

#include <cstdio>
#include <cstdlib>
#include <climits>
#include <cstring>

const int MAX = 550;

const int type[11] = {3,6,9,12,10,5,7,11,13,14,15};
const int dirx[4] = {0,-1,0,1},diry[4]={-1,0,1,0};
int m,n;
char farm[MAX][MAX];
int visit[MAX][MAX];

bool yes(int ax,int ay,int bx,int by,int dir){
	bool mark = false;
	int ta,tb;

	if(bx<1 || bx>n || by<1 || by>m)return false;
	ta = farm[ax][ay]-'A';
	tb = farm[bx][by]-'A';

	if(dir==0){//向左
		if((type[ta] & 1) && ((type[tb]>>2) & 1))mark = true;
	}else if(dir==1){//向上推断可连性
		if(((type[ta]>>1) & 1) && ((type[tb]>>3) & 1))mark = true;

	}else if(dir==2){//水平向右
		if(((type[ta]>>2) & 1) && (type[tb] & 1))mark = true;
	}else{//水平向下推断可连性
		if(((type[ta]>>3) & 1) && ((type[tb]>>1) & 1))mark = true;
	}
	return mark;
}

void dfs(int x,int y){
	if(visit[x][y])return;
	visit[x][y] = 1;
	int tx,ty,i;
	for(i=0;i<4;++i){
		tx = x + dirx[i];
		ty = y + diry[i];
		if(yes(x,y,tx,ty,i)){
			dfs(tx,ty);
		}
	}
}

int main(){
	//freopen("in.txt","r",stdin);
	int i,j,ans;
	while(scanf("%d %d",&n,&m)!=EOF){
		if(n==-1 && m==-1)break;
		ans = 0;
		memset(visit,0,sizeof(visit));
		for(i=1;i<=n;++i){
			scanf("%s",farm[i]+1);
		}
		for(i=1;i<=n;++i){
			for(j=1;j<=m;++j){
				if(visit[i][j])continue;
				++ans;
				dfs(i,j);
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}

版权声明：本文博主原创文章，博客，未经同意不得转载。