POJ1661(KB12-M DP)

Help Jimmy

Description

"Help Jimmy" 是在下图所示的场景上完成的游戏。 

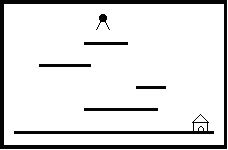
场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。

Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。

设计一个程序，计算Jimmy到底地面时可能的最早时间。

Input

第一行是测试数据的组数t（0 <= t <= 20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i = 1..N）。所有坐标的单位都是米。

Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。

Output

对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。

Sample Input

1
3 8 17 20
0 10 8
0 10 13
4 14 3

Sample Output

23

Source

POJ Monthly--2004.05.15 CEOI 2000

 

 //2017-04-06
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>

 using namespace std;

 const int inf = 0x3f3f3f3f;
 struct node{
     int l, r, h;
     bool operator<(const node x)
     {
         return this->h > x.h;
     }
 }platform[];
 int dpl[], dpr[];//dpl[i]记录从第i块平台左端点落地所需的最短时间,dpr[i]记录从第i块平台右端点落地所需的最短时间
 int n, MAX;

 int dfs(int x, int y, int ptr)//输入参数表示从第ptr块平台，位于(x, y)点开始搜索
 {
     if(dpl[ptr] != inf && dpr[ptr] != inf)
       if(y-platform[ptr].h <= MAX)
         if(platform[ptr].l <= x && platform[ptr].r >= x)
           return y-platform[ptr].h+min(dpl[ptr]+x-platform[ptr].l, dpr[ptr]+platform[ptr].r-x);//记忆化搜索，返回位于(x, y)点向左右走的最短时间
     int l, r, h;
     for(int i = ptr; i < n; i++){
         l = platform[i].l;
         r = platform[i].r;
         h = platform[i].h;
         if(h <= y && y-h <= MAX){
             if(x >= l && x <= r){
                 if(h == )return y-h;
                 else{
                     int left = dfs(l, h, i+);//向左走
                     dpl[i] = min(dpl[i], left);
                     int right = dfs(r, h, i+);//向右走
                     dpr[i] = min(dpr[i], right);
                     return y-h+min(dpl[i]+x-l, dpr[i]+r-x);
                 }
             }
         }
     }
     return inf;
 }

 int main()
 {
     int T, x, y, ans;
     scanf("%d", &T);
     while(T--)
     {
         scanf("%d%d%d%d", &n, &x, &y, &MAX);
         for(int i = ; i < n; i++){
             scanf("%d%d%d", &platform[i].l, &platform[i].r, &platform[i].h);
             dpl[i] = dpr[i] = inf;
         }
         //加入地面这一块平台，高度为0，左右边界无穷
         platform[n].h = ;
         platform[n].l = -inf;
         platform[n].r = inf;
         dpl[n] = dpr[n] = inf;
         n++;
         sort(platform, platform+n);
         int l, r, h, i;
         for(i = ; i < n; i++)//找到下落遇到的地一块平台，从这块平台开始搜索
         {
             l = platform[i].l;
             r = platform[i].r;
             h = platform[i].h;
             if(h <= y && y-h <= MAX)
               if(x >= l && x <= r)
                 break;
         }
         ans = dfs(x, h, i)+y-h;
         printf("%d\n", ans);
     }

     return ;
 }