SVM-支持向量机（三）SVM回归与原理

SVM回归

我们之前提到过，SVM算法功能非常强大：不仅支持线性与非线性的分类，也支持线性与非线性回归。它的主要思想是逆转目标：在分类问题中，是要在两个类别中拟合最大可能的街道（间隔），同时限制间隔侵犯（margin violations）；而在SVM回归中，它会尝试尽可能地拟合更多的数据实例到街道（间隔）上，同时限制间隔侵犯（margin violation，也就是指远离街道的实例）。街道的宽度由超参数ϵ控制。下图展示的是两个线性SVM回归模型在一些随机线性数据上训练之后的结果，其中一个有较大的间隔(ϵ = 1.5)，另一个的间隔较小(ϵ = 0.5)。

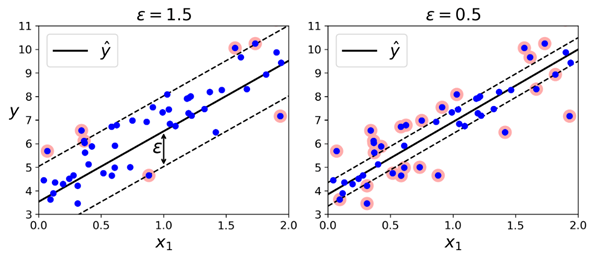
如果后续增加的训练数据包含在间隔内，则不会对模型的预测产生影响，所以这个模型也被称为是ϵ-insensitive。

我们可以使用sk-learn的LinearSVR类训练一个SVM回归，下面的代码对应的是上图中左边的模型（训练数据需要先做缩放以及中心化的操作，中心化又叫零均值化，是指变量减去它的均值。其实就是一个平移的过程，平移后所有数据的中心是(0, 0)）：

from sklearn.svm import LinearSVR

svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)

再处理非线性的回归任务时，也可以使用核化的SVM模型。例如，下图展示的是SVM回归在一个随机的二次训练集上的表现，使用的是二阶多项式核：

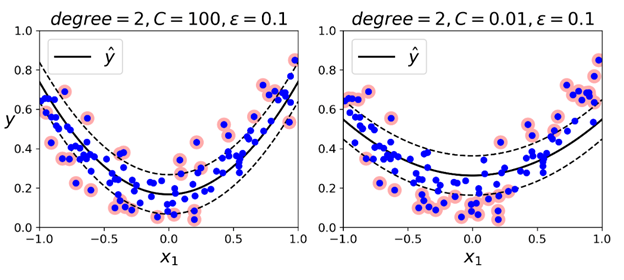
左边的图中有一个较小的正则（超参数C的值较大），而右边图中的正则较大（较小的C值）。

下面的代码上图中左边的图对应的模型，使用的是sk-learn SVR类（支持核方法）。SVR类等同于分类问题中的SVC类，并且LinearSVR类等同于分类问题中的LinearSVC类。LinearSVR类会随着训练集的大小线性扩展（与LinearSVC类一样）；而SVR类在训练集剧增时，速度会严重下降（与SVC类一致）：

from sklearn.svm import SVR

svm_poly_reg = SVR(kernel='poly', degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X, y)

SVMs也可以用于异常点（值）检测，具体可以参考sk-learn文档。

原理解释

在这章我们会解释SVM如何做预测，以及训练算法是如何工作的，先从线性SVM分类器开始。

首先，我们将所有的模型参数放入一个向量θ，包括偏置项参数θ₀以及输入特征的权重θ₁ 到 θ_n，并且给所有数据实例增加一个偏置项x₀ = 1。这里偏置项称为b，特征权重向量称为w。

决策方法与预测

线性SVM分类器模型在做预测时，对于输入的实例x，它会计算决策函数wTx + b = w₁x₁ + ⋯ + w_nx_n + b：如果结果是正的，则预测的类别ŷ就属于正类(1)，否则属于反类(0)，如下公式所示：

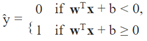
下面我们看一下SVM在之前iris数据集上训练后的决策函数图：

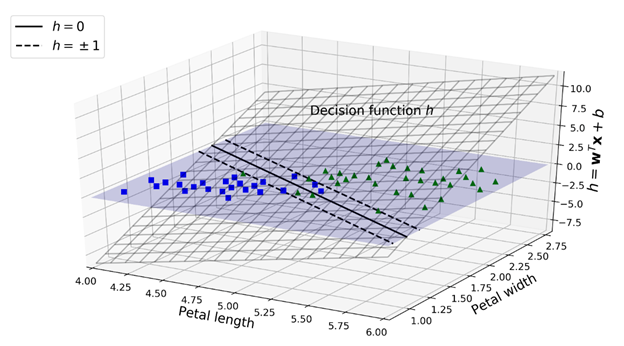
这是一个二维平面，因为数据集有两个特征（petal width与petal length）。决策边界是由那些让决策函数等于0的点组成：也就是两个平面的交线（由上图中实线表示）。

虚线代表的是令决策函数等于1或-1的点：这两条虚线平行且距决策边界的距离相等，组成了一个间隔。训练线性SVM分类器就是找到一对w与b的值，让这个间隔尽可能的宽的同时，还要避免或是限制间隔侵犯（margin violation）。避免间隔侵犯的结果就是硬间隔（hard margin），限制间隔侵犯的结果就是软间隔（soft margin）。

训练目标

上图的例子中我们看到这个决策函数的图像是一个平面，并且有一个坡度。这个坡度等同的是权重向量w的范数（norm）：∥ w ∥。如果我们将这个坡度除以2，则那些令决策函数等于±1 的点会离决策边界两倍远。换句话说，坡度除以2会让间隔增加2倍。如下图所示：

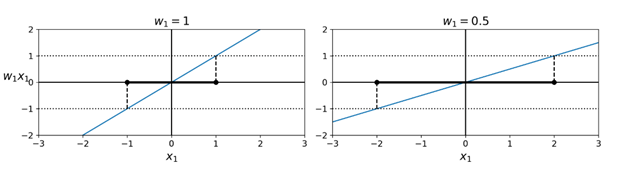
所以我们希望最小化 ∥ w ∥ 的值以获取一个更大的间隔。不过，如果我们同时也希望避免间隔入侵（硬间隔），则我们需要让决策函数对所有训练数据中的“正”训练实例计算结果大于1，而对所有“负”训练实例的计算结果小于-1。如果我们对负实例（也就是y⁽ⁱ⁾ = 0）定义t⁽ⁱ⁾ = –1，对正实例（y⁽ⁱ⁾ = 1）定义t⁽ⁱ⁾ = 1，则我们可以使用约束t⁽ⁱ⁾(w^T x⁽ⁱ⁾ + b) ≥ 1 定义所有实例。

所以我们接下来可以将硬间隔SVM分类器目标表示为一个带约束的优化问题，如下公式：

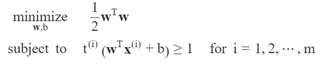
这里可以看到，我们优化的不是∥ w ∥，而是½w^Tw，它等同于½∥ w ∥²。因为½∥ w ∥²的导数非常简单（也就是w），而∥ w ∥ 在w=0时不可微。优化算法在可微函数上工作效果更好。

为了达到软间隔（soft margin）目标，我们需要为每个实例i引入一个松弛变量ζ(i) ≥ 0，这个变量衡量的是第i^th个实例被允许入侵间隔的程度。我们现在有两个冲突的目标：让松弛变量尽可能的小，以减少间隔入侵；同时还要让 ½∥ w ∥² 尽可能的小，以增加间隔。所以这就是为什么算法中引入超参数C：这个参数可以让我们定义这两个目标之间的权衡（tradeoff）。对应的带约束优化问题为：

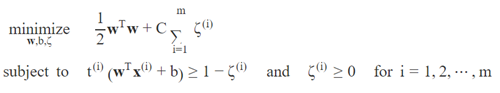
二次规划

硬间隔与软间隔问题都是带线性约束的凸二次优化问题，这种就是常说的二次规划（Quadratic Programming，QP）问题。有很多现成的解决办法用于解决QP问题，在这不会深入讨论。这种常规问题的公式如下所示：

需要注意的是表达式Ap ≤ b 定义了n_c的约束：p^⊺ a⁽ⁱ⁾ ≤ b⁽ⁱ⁾ for i = 1, 2, ⋯, n_c, 这里a⁽ⁱ⁾代表的是包含了A的第i^th行的向量，b⁽ⁱ⁾代表的是b的i^th第个元素。

如果我们按下面的参数设置QP参数，则可以得到硬间隔线性SVM分类器的目标：

一个训练硬间隔线性SVM分类器的方法是使用已有的OP问题解决方法，传入上述参数即可。求得的结果向量p会包含偏执项b=p₀，以及特征权重w_i = p_i for i = 1, 2, ⋯, n。类似的，也可以使用QP问题解决方案解决软间隔问题。

不过在使用核方法时，我们会使用另一个不同的带约束的优化问题。

在线SVM（online SVM）

在这章结束之前，我们快速地看一下在线SVM分类器（在线学习是指递增的训练，一般在一个新实例到达时就训练一次）。

对于线性SVM分类器，一种方法是使用梯度下降（例如使用SGDClassifier）最小化以下损失函数：

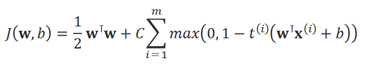
这个损失函数是由原始问题推导得出，但是它的收敛速度相比基于QP方法的收敛会慢特别多。在这个损失函数中，第一个累加会推进模型去找一个较小的权重向量w，继而产生一个更大的间隔。第二个累加会计算所有的间隔入侵（margin violations）。一个实例如果是远离街道、且在它所属正确的那一侧，则它的间隔入侵为0；否则它的间隔入侵则为距离正确那一侧街道的距离的比例。最小化这个项，会确保模型尽可能少地造成间隔入侵。

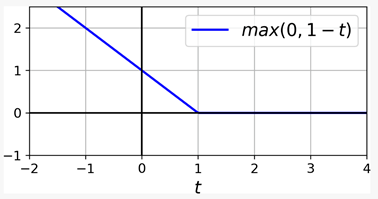
最后提一下HINGE LOSS，我们之前在训练SVM时使用的是这个损失函数。它的函数为max(0, 1-t)。在 t ≥ 1时，输出为0。它的导数在t < 1 时等于 -1，在t > 1 时等于0 ；在t=1时不可微，不过仍可以在使用梯度下降时，使用t=1 时的任何次导数（也就是说，任何在-1到0之间的值）。函数图如下：

在在线SVM中，也是可以实现在线核化SVM的，例如使用“Incremental and Decremental SVM Learning” 或”Fast Kernel Classifiers with Online and Active Learning”。不过这些是通过Matlab和C++实现的。对于大型的非线性问题，我们其实可以考虑使用神经网络。