Codeforces Round #614 (Div. 2) A-E简要题解

链接：https://codeforces.com/contest/1293

A. ConneR and the A.R.C. Markland-N

题意：略

思路：上下枚举1000次扫一遍，比较一下上下最近的房间

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<map>
 #include<utility>
 #include<string>
 #include<vector>
 #include<cstring>
 #include<iostream>
 #include<vector>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<cstdio>
 #include<unordered_map>
 using namespace std;
 const int maxn=1e5;
 typedef long long ll;

 int main()
 {
     int t;
     cin >> t;
     while(t--)
     {
         map<int,int> v;
         int n,s,k;
         scanf("%d%d%d",&n,&s,&k);
         int x;
         for(int i=; i<=k; i++)
         {

             scanf("%d",&x);
             v[x]++;
         }
         int l,r;
         l=r=s;
         if(!v[s])
             cout <<  << endl;
         else
         {
             while(v[l]&&v[r])
             {
                 if(l->=)
                     l--;
                 if(r+<=n)
                     r++;

             }
             if(!v[r]&&!v[l])
             {
                 cout << min(s-l,r-s) << endl;
             }
             else if(!v[r]&&v[l])
             {
                 cout << r-s<< endl;
             }
             else if(v[r]&&!v[l])
                 cout << s-l << endl;
         }
     }
     return ;
 }

B. JOE is on TV!

题意：略

思路：比较简单，推结论 max （n） = i/n+(i-1)/n + ...n/n

AC代码：

 #include<iostream>
 #include<vector>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<cstdio>
 #include<unordered_map>
 using namespace std;
 typedef long long ll;
 int main(){
     int t;
     float ans = ;
     scanf("%d",&t);
     float i = ;
     while(i<=t){
         ans+=(/i);
         i+=;
     }
     printf("%.12lf",ans);
     return ;
 }

C. NEKO's Maze Game

题意：有一个2×n的网格迷宫，网格可以翻动，由正常区域和堵塞区域切换，问从（1，1）能否到（2，n）

思路：一个网格如果翻动，如果这个网格是在第二列，那么这个网格可以和其左上角、正上方、右上角构成堵塞，这样算是三个“堵塞贡献”，如果位于第一列翻动由正常区域变成堵塞，那么这个网格可以和左下角、正下方、右下方的网格构成堵塞区域，这样也是三个贡献，每次放置网格就计算上这些贡献，换回正常的时候就减去，如果总的贡献是0，那么就可以到达（2，n）

AC代码：

 #include<iostream>
 #include<vector>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 #include<queue>
 #include<cstdio>
 #include<unordered_map>
 using namespace std;
 typedef long long ll;
 const int maxn = 1e5+;
 int grid[][maxn];
 int can[maxn];
 int main(){
     int n,q;
     int cnt = ;
     scanf("%d%d",&n,&q);
     while(q--){
         int x,y;
         scanf("%d%d",&x,&y);
         x = x - ;
         if((grid[][y]+grid[][y]) == ){
             cnt--;
         }
         if(grid[x][y]+grid[(x+)%][y-] == ){
             cnt--;
         }
         if(grid[x][y]+grid[(x+)%][y+] == ){
             cnt--;
         }
         grid[x][y] = (grid[x][y]+)%;
         if((grid[][y]+grid[][y]) ==  ){
             cnt++;
         }
         if(grid[x][y]+grid[(x+)%][y-] ==  ){
             cnt++;
         }
         if(grid[x][y]+grid[(x+)%][y+] ==  ){
             cnt++;
         }
         if(cnt == ){
             printf("YES\n");
         }
         else printf("NO\n");
     }
     return ;
 }

D. Aroma's Search

题意：二维平面上有若干个点，第i个点的坐标(xi,yi)满足xi=xi-1*ax+bx,yi=y-1*ay+by，已知 ax,bx,ay,by,x0,y0 以及初始位置(xs,ys)，每秒钟可以往上下左右走1个单位，则在t秒内最多可以走到多少个点

思路：所有点之间的曼哈顿距离是乘指数级别增长的，不能到了一个点之后再回到初始点，也不能从距离最近的点开始出发去枚举。考虑到数据范围，其实点的极限数量大概在60多，所以可以构造一个暴力的算法去枚举。最佳的方案是先从起点到其中一个点，再从这个点向下面的点移动，因为向上比向下距离远，如果下方所有的点都可以到达，再往上走，这样是最佳的方案。所有需要枚举起点到每一个点，再从该点先向下方移动再向上移动

AC代码：

     #include<bits/stdc++.h>
     using namespace std;
     typedef long long ll;
     ll x0,y0,ax,ay,bx,by,xs,ys,t;
     vector<pair<ll,ll> > v;
     ll solve(int x){
         ll remain = t;
         remain -= abs(v[x].first-xs)+abs(v[x].second-ys);
         if(remain<) return ;
         ll res = ;
         int last = x;
         for(int i = x-;i>=;i--){
             ll can = abs(v[i].first-v[last].first)+abs(v[i].second-v[last].second);//先向下方的点移动
             if(remain-can<) break;
             res++;
             remain-=can;
             last = i;
         }
         for(int i = x+;i<v.size();i++){
             ll can = abs(v[i].first-v[last].first)+abs(v[i].second-v[last].second);//如果还有时间剩余向上方点移动
             if(remain-can<) break;
             res++;
             remain-=can;
             last = i;
         }
         return res;
     }
     int main(){
         cin>>x0>>y0>>ax>>ay>>bx>>by;
         cin>>xs>>ys>>t;
         ll curx = x0,cury = y0;
         while(){
             ll disX = abs(curx-xs);
             ll disY = abs(cury-ys);
             if(curx>xs && cury>ys && disX+disY > t) break;//如果移动到该点就超过了t秒，break
             v.push_back({curx,cury});
             curx = ax*curx+bx;
             cury = ay*cury+by;
         }
         ll ans = ;
         for(int i = ;i<v.size();i++){
             ans = max(ans,solve(i));//枚举到每个点
         }
         cout<<ans;
         return ;
     }

E. Xenon's Attack on the Gangs

题意：给出一颗树，树上随机分配边权值，不存在权值相同的两条边，定义mex（u，v）表示点u到点v经过边的边权集合S中没有出现的最小非负整数，求S = ∑mex（u，v） （1<=u<=v<=n）的最大值。

思路：这道题没有太明白，看官方题解首先要推出一个组合公式，问题转化为求一条边的贡献，对u到v的路径进行dp，枚举u到v的每一条路径的贡献。

放个官方题解吧

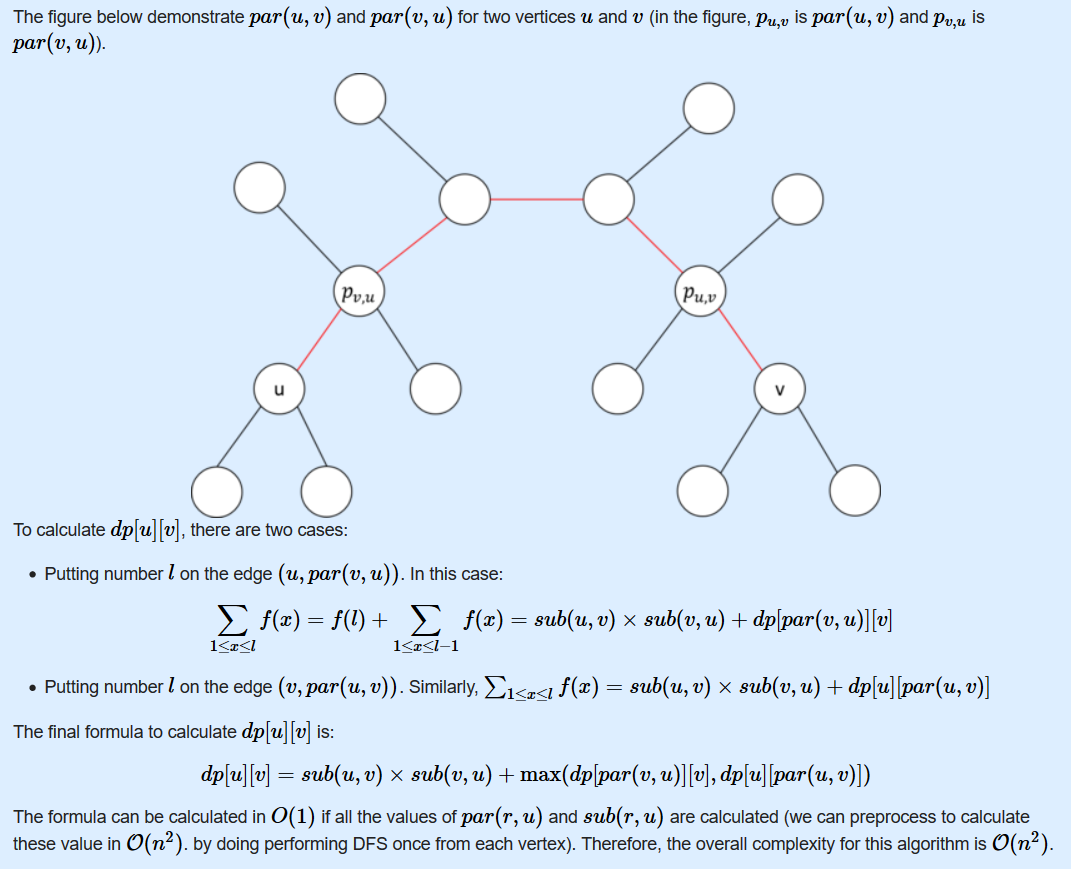
AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn = ;
 typedef long long ll;
 int fa[maxn][maxn],sub[maxn][maxn];
 ll dp[maxn][maxn];
 vector<int> G[maxn];
 int n,root;
 int dfs(int cur,int father){
     sub[root][cur] = ;
     for(int i = ;i<G[cur].size();i++){
         if(G[cur][i]!=father){
             fa[root][G[cur][i]] = cur;
             sub[root][cur]+=dfs(G[cur][i],cur);
         }
     }
     return sub[root][cur];
 }
 ll getDp(int u,int v){
     if(u == v) return ;
     if(dp[u][v] ) return dp[u][v];
     return dp[u][v] = sub[u][v]*sub[v][u] + max(getDp(fa[v][u],v),getDp(fa[u][v],u));
 }
 int main(){
     scanf("%d",&n);
     for(int i = ;i<n;i++) {
         int u,v;
         cin>>u>>v;
         G[u].push_back(v),G[v].push_back(u);
     }
     for(int i = ;i<=n;i++){
         root = i;
         dfs(i,-);
     }
     ll res = ;
     for(int i = ;i<=n;i++){
         for(int j = ;j<=n;j++){
             res = max(res,getDp(i,j));
         }
     }
     printf("%lld",res);
     return ;
 }