Codeforces 306D - Polygon（随机化+乱搞）

Codeforces 题目传送门 & 洛谷题目传送门

中考终于结束了……简单写道题恢复下状态罢。

首先这一类题目肯定没法用一般的方法解决，因此考虑用一些奇淫的乱搞做法解决这道题，不难发现，如果我们固定住了前 \(n-1\) 条边，那么第 \(n\) 条边的长度与前 \(n-1\) 条边的长度冲突的概率是小之又小了——这个用爪子想想即可明白。

因此考虑一个乱搞做法，我们每次随机前 \(n-1\) 条边的长度 \(l_1,l_2,\cdots,l_{n-1}\)，然后从原点开始绕一圈每次旋转 \(\dfrac{2\pi}{n}\) 补全这个 \(n\) 边形，如果最后一条边的长度与前 \(n-1\) 条边长度均不同且在 \((0,1000]\) 之内则直接输出。

这样一来倒是避免边长度相同的问题了，但同时还会带来另一个问题，就是如果有可能我们随机出来的图形不是凸图形，比如说下图：

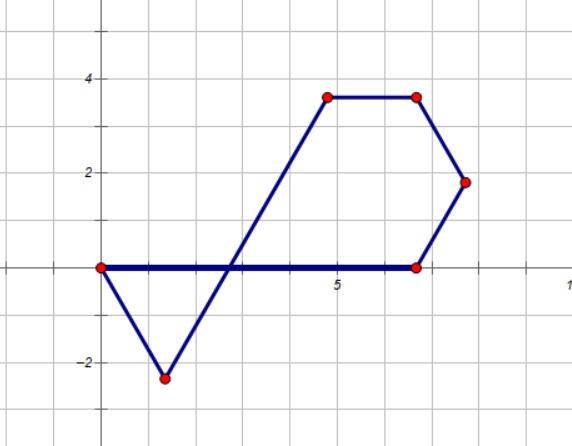
解决方法倒也容易，把每条边随机的范围变小一点即可，我是将第 \(i\) 条边的长度设为 \(600+0.1i\) 然后 random_shuffle，这样就不太可能出现这样的情况了。

思路出来了，剩下就是实现的问题了，旋转 \(\dfrac{2\pi}{n}\) 我拿复数乘法实现的，最后第 \(n\) 个点的位置需解个直线方程。

随机次数最多大概是 \(2\)（别问我怎么知道的 qwq），时间复杂度 \(\mathcal O(\text{能过)}\)

const int MAXN=100;
const double Pi=acos(-1);
const double EPS=1e-6;
int n;
double len[MAXN+5];
struct point{
	double x,y;
	point(double _x=0,double _y=0):x(_x),y(_y){}
	point operator +(const point &rhs) const{return point(x+rhs.x,y+rhs.y);}
	point operator -(const point &rhs) const{return point(x-rhs.x,y-rhs.y);}
	point operator *(const double &rhs) const{return point(x*rhs,y*rhs);}
	point operator /(const double &rhs) const{return point(x/rhs,y/rhs);}
	double operator ~() const{return sqrt(x*x+y*y);}
} p[MAXN+5];
int main(){
	srand(time(0));scanf("%d",&n);
	if(n<=4) return puts("No solution")&0;
	double ang=2*Pi/n;
	while(1){
		for(int i=1;i<n;i++) len[i]=600+i*0.1;
		random_shuffle(len+1,len+n);
		p[1]=point(0,0);p[2]=point(len[1],0);
		for(int i=3;i<=n;i++){
			point dif=p[i-1]-p[i-2];
			point coe=point(cos(ang),sin(ang));
			point nw=point(dif.x*coe.x-dif.y*coe.y,dif.x*coe.y+dif.y*coe.x);
			nw=nw*(len[i-1]/len[i-2]);
			if(i^n) p[i]=p[i-1]+nw;
			else{
				double k1=nw.y/nw.x;
				double b=p[i-1].y-k1*p[i-1].x;
				double k2=tan(Pi/n*(n-2));
				p[i].x=b/(k2-k1);p[i].y=k2*p[i].x;
			}
		} bool flg=(~(p[1]-p[n])<1000+EPS);
		for(int i=1;i<n;i++) flg&=(fabs((~(p[1]-p[n]))-len[i])>EPS);
		if(flg) break;
	}
	for(int i=1;i<=n;i++) printf("%.10lf %.10lf\n",p[i].x,p[i].y);
	return 0;
}