Full Regularization Path for Sparse Principal Component Analysis

目录

• 背景
• Notation
• Sparse PCA
• Semidefinite Relaxation
• Low Rank Optimization
• Sorting and Thresholding

背景

懒得说了，毕竟和上一篇作者都是一个人，有特殊的情况是，上次做的复杂度过大，这次降低了复杂度。

Notation

Sparse PCA

在上篇论文里面，也提到了这个式子。上次是用它来进行一个robust的解释，这一次，是来试图解决这个问题。

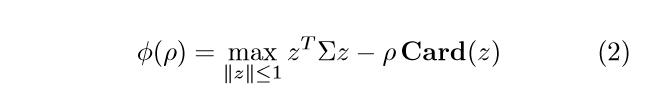
\(\Sigma_{ii} \quad i=1,2,\ldots,n\)，为\(\Sigma\)的特征值，且降序排列。
首先，考虑，\(\rho > \Sigma_{11}\)的时候，

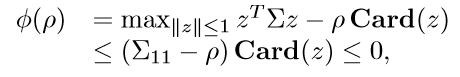
所以，\(z=0\)
再考虑, \(\ro < \Sigma_{11}\),令\(u\in\{0, 1\}^{n}\)

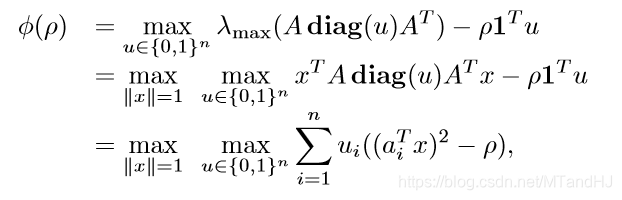
通过最大化\(u\)，可得

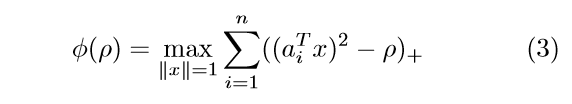
Semidefinite Relaxation

为了求解上面的问题，需要做一些改变，和上篇论文，思想差不多。

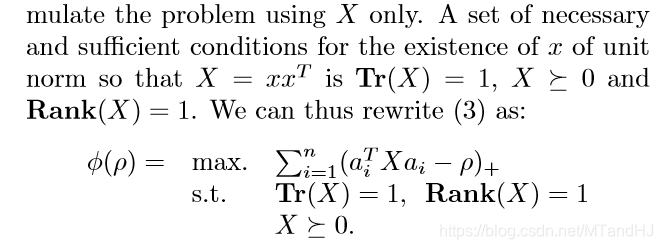
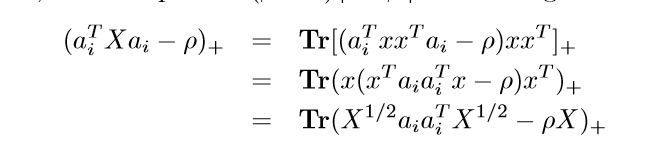
问题是凸的不是凹的，这样没法求最大值。所以（其实没怎么懂），改，

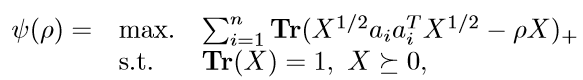
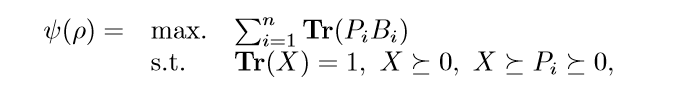
Low Rank Optimization

但是呢，求解这个问题比较费时，所以又转换思路，欲将\(X\)分解，从这以后，我就没怎么看了，所以也不怎么懂（估计看了也不怎么懂。）

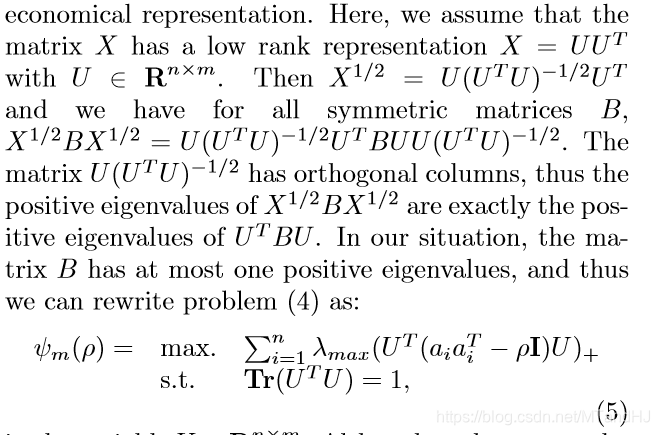
Sorting and Thresholding

这里讲怎么选特征？

为了节省计算成本，做了一些改进：

反正我觉得上面俩种方法都蛮蠢的。