recursion 递归以及递归的缺点

递归定义的算法有两部分：

递归基：直接定义最简单情况下的函数值；

递归步：通过较为简单情况下的函数值定义一般情况下的函数值。

应用条件与准则：

（1）问题具有某种可借用的类同自身的子问题描述的性质；

（2）某一问题有限步的子问题（也称做本原问题）有直接的解存在。

在计算机中是利用栈来实现recursion的，对于每一次递归的调用，计算机都会将调用者的局部变量以及返回地址储存在栈中，待回调时恢复局部变量，并返回到调用地址中

正因计算机会保存所有的局部变量，这将导致额外的开销，使程序运行效率底下，我们可以拿计算斐波那契数列作例子

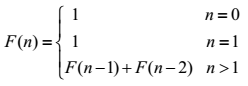
由此形式读者很容易想到用递归解决问题，但这往往是一个陷进

当n!=0||n!=0时，我们将要执行，在F（n-1）中又要执行F（n-2）+F（n-3），在F（n-2）中执行F（n-3）+F（n-4），要掉用以及保存的变量数量呈级数式的增长，同时其中又存在许多重复的，这么做个程序带来了额外的开销，显得recursion效率低下

下面我们来具体比较一下

#include<iostream>
#include<ctime>
using namespace std;

//递归
int recursion(int n)
{
	if(n==1||n==2)
		return 1;
	else
		return recursion(n-1)+resursion(n-2);
}

//迭代
int iteration(int n)
{
	int p1=1;
	int p2=1;
	while(n->2)
	{
        int temp=p2;
		p2=p1+p2;
		p1=temp;
	}
     return p2;
}

int main()
{
	int n;
	cin>>n;

	clock_t start=clock();
    recursion(n);
    clock_t end=clock();
	cout<<"Recursion 用时: "<< start-end << endl;

	start=clock();
    iteration(n);
    end=clock();
	cout<<"iteration 用时: "<< start-end << endl;

    return 0;
}