LG3187 [HNOI2007]最小矩形覆盖

题意

题目描述

给定一些点的坐标，要求求能够覆盖所有点的最小面积的矩形，输出所求矩形的面积和四个顶点坐标

输入输出格式

输入格式：

第一行为一个整数n（3<=n<=50000），从第2至第n+1行每行有两个浮点数，表示一个顶点的x和y坐标，不用科学计数法

输出格式：

第一行为一个浮点数，表示所求矩形的面积（精确到小数点后5位），接下来4行每行表示一个顶点坐标，要求第一行为y坐标最小的顶点，其后按逆时针输出顶点坐标.如果用相同y坐标，先输出最小x坐标的顶点

输入输出样例

输入样例#1：
复制

6 1.0 3.00000
 
1 4.00000
 
2.0000 1
 
3 0.0000
 
3.00000 6
 
6.0 3.0

输出样例#1：
复制

18.00000
 
3.00000 0.00000
 
6.00000 3.00000
 
3.00000 6.00000
 
0.00000 3.00000

说明

感谢 @intruder 提供题目简述

分析

参照wzq_QwQ的题解。

先求凸包，然后求最小矩形覆盖。

有一个显而易见的结论：选择的最小矩阵一定有一条边与凸包上的一条边重合。

我们可以枚举在矩阵上的这个边，然后再以这条边找到卡住的相对的最左边的点以及最右边的点，和相对的最上面的点。

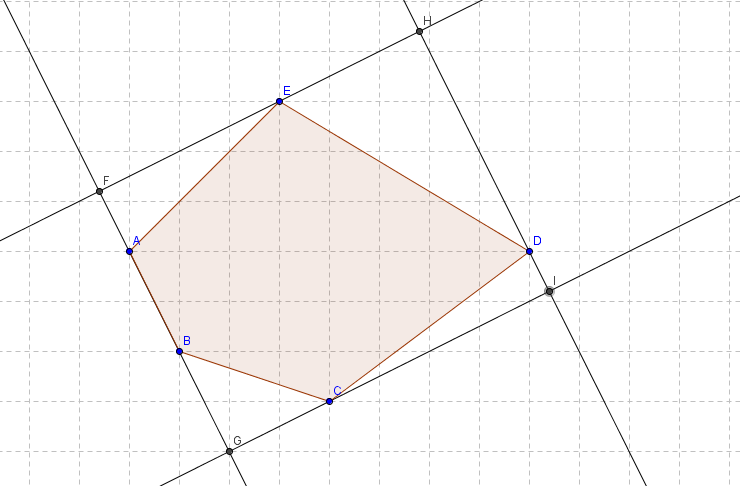
画个图

假设我们枚举到了AB这条边。

然后目前的相对的最右边的点是点C，相对的最左边的点是点E，相对的最高点时点D。

先说怎么卡壳的吧。

首先对于最右边的点来说，卡(qia)的是点积最大，最左边的呢卡的是点积最小的，但是注意一个问题，第一次卡(qia)的时候这个最左边的一定是最高点的后面的点，这是很显然的，

不然我们如果遇到前面有点积相同的时候是卡不过去的。

所以第一次卡的时候要把最左边的点从最高点开始转。

最高点显然就是叉积最大嘛..

因为有叉积，我们可以求出来这个矩阵的宽的长度。

长怎么求呢？

利用点积。

我们知道AB的线段长，又知道向量AB与向量AE的点积，所以我们能求出来AE在AB方向上的投影。

于是就知道FA

同理右边可求。

然后现在我们求出来了矩阵长和宽，所以就能知道第一问面积了。

但是第二问怎么办呢？我们知道点A的坐标，考虑从向量AB的方向开始逆时针找矩阵的四个定点。其实就是把向量乘一下

AG我们都知道，所以就把AB乘成AG就知道G。

其余的同理。

时间复杂度\(O(n \log n)\)

代码

注意会输出-0这种情况。

#include<algorithm>
#include<cstdio>
#include<cmath>
#define co const
using namespace std;
co double eps=1e-8;
typedef struct Point{double x,y;}Vector;
bool operator<(co Point&u,co Point&v) {return u.x<v.x||u.x==v.x&&u.y<v.y;}
Vector operator+(co Vector&u,co Vector&v) {return (Vector){u.x+v.x,u.y+v.y};}
Vector operator-(co Vector&u,co Vector&v) {return (Vector){u.x-v.x,u.y-v.y};}
double cross(co Vector&u,co Vector&v) {return u.x*v.y-u.y*v.x;}
double dot(co Vector&u,co Vector&v) {return u.x*v.x+u.y*v.y;}
double length(co Vector&u) {return sqrt(dot(u,u));}
Vector operator*(co Vector&u,double k) {return (Vector){u.x*k,u.y*k};}
co int N=5e4+1;
int n,m;
Point p[N],ch[N*2],print[4];
double Rotating_Calipers(){
    double ans=1e18;
    int p=1,q=1,r=1;
    for(int i=0;i<m;++i){
        Vector u=ch[i+1]-ch[i];
        double lu=length(u);
        while(dot(u,ch[p+1]-ch[i])-dot(u,ch[p]-ch[i])>-eps) p=(p+1)%m;
        while(cross(u,ch[r+1]-ch[i])-cross(u,ch[r]-ch[i])>-eps) r=(r+1)%m;
        if(!i) q=r;
        while(dot(u,ch[q+1]-ch[i])-dot(u,ch[q]-ch[i])<eps) q=(q+1)%m;
        double R=dot(ch[p]-ch[i],u)/lu;
        double L=fabs(dot(ch[q]-ch[i],u)/lu);
        double leng=L+R;
        double heig=cross(u,ch[r]-ch[i])/lu;
        if(ans>leng*heig){
            ans=leng*heig;
            print[0]=ch[i]+u*(R/lu);
            print[1]=print[0]+(ch[p]-print[0])*(heig/length(ch[p]-print[0]));
            print[2]=print[1]+(ch[r]-print[1])*(leng/length(ch[r]-print[1]));
            print[3]=print[2]+(ch[q]-print[2])*(heig/length(ch[q]-print[2]));
        }
    }
    return ans;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i) scanf("%lf%lf",&p[i].x,&p[i].y);
    sort(p+1,p+n+1);
    for(int i=1;i<=n;++i){
        while(m>=2&&cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) --m;
        ch[m++]=p[i];
    }
    for(int k=m,i=n-1;i>=1;--i){
        while(m>=k+1&&cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) --m;
        ch[m++]=p[i];
    }
    if(n>1) --m;
    printf("%.5lf\n",Rotating_Calipers());
    int pre=0;
    for(int i=1;i<=3;++i)
        if(print[i].y<print[pre].y||fabs(print[i].y-print[pre].y)<eps&&print[i].x<print[pre].x) pre=i;
    for(int i=0;i<4;++i) {
        if(fabs(print[(pre+i)%4].x)<eps) print[(pre+i)%4].x=0;
        if(fabs(print[(pre+i)%4].y)<eps) print[(pre+i)%4].y=0;
        printf("%.5lf %.5lf\n",print[(pre+i)%4].x,print[(pre+i)%4].y);
    }
}