Luogu P1318 积水面积

题目描述

一组正整数，分别表示由正方体迭起的柱子的高度。若某高度值为x，表示由x个正立方的方块迭起（如下图，0<=x<=5000）。找出所有可能积水的地方（图中蓝色部分），统计它们可能积水的面积总和（计算的是图中的横截面积。一个立方体的位置，为一个单位面积）。

如图：柱子高度变化为 0 1 0 2 1 2 0 0 2 0

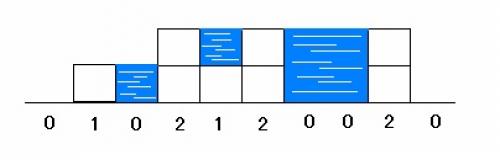
图中蓝色部分为积水面积，共有6个单位面积积水。

输入输出格式

输入格式

两行，第一行n,表示有n个数(3<=n<=10000)。第2行连续n个数表示依次由正方体迭起的高度，保证首尾为0。

输出格式

一个数，可能积水的面积。

思路

首先，去前导后导零，并更新l与r，然后对于柱高做一遍前缀和（优化用）。
对于每个柱子，我们分两种情况考虑

第一种：后面有柱子比它来得高，那就取离它最近且比它高的柱子为断点，更新S的值\(（S+=min(h[i],h[l])*(i-l-1)-(sum[i-1]-sum[l]); ）\)，将l更新至断点处，然后将flag定为1，表示有柱子比他高。

第二种：如果flag=0，后面没有柱子比它高，那就取之后柱子中最高的一个做断点（设位置为WZ），然后更新S的值（h[wz]一定比h[l]小）\(（S+=h[wz]*(wz-l-1)-(sum[wz-1]-sum[l]);）\)，最后将l更新到断点处（l=WZ）

最后当l>=r时退出输出S即可

代码

#include<bits/stdc++.h>
using namespace std;
int n,h[10005],l,r,sum[10005],S=0;
int main()
{
    scanf("%d",&n);
    l=1;r=n;
    for (int i=1;i<=n;i++) scanf("%d",&h[i]),sum[i]=sum[i-1]+h[i];
    while (!h[l]) l++; while (!h[r]) r--;
    while (l<r)
    {
        if (l==r) break;
        bool flag=0;
        for (int i=l+1;i<=n;i++)
        if (h[i]>=h[l])
        {
         flag=1;
         S+=min(h[i],h[l])*(i-l-1)-(sum[i-1]-sum[l]);
         l=i;
         break;
        }
        if (flag==0)
        {
            int maxx=0,wz;
            for (int i=l+1;i<=n;i++) if (h[i]>maxx) wz=i,maxx=h[i];
            S+=h[wz]*(wz-l-1)-(sum[wz-1]-sum[l]);
            l=wz;
        }
    }
    cout<<S<<endl;
    return 0;
}