Vue学习系列---安装

一、前言

　　学任何东西都是有理由的，目前主要有Angular，React，Vue这三个前端MVVM框架。我选择vue原因很简单，“”入门简单“”，是的只是这个理由。相较于其他2个框架，vue的文档真的是太亲民的，入门曲线没有那么陡，对于我这种小菜鸟来说，是入门首选。等vue熟悉后，相信再看别的前端MVVM框架也是一通百通的效果。

　　目前流行的2套基于vue.js的UI框架element-ui(http://element-cn.eleme.io/#/zh-CN/component/installation)和Iview(https://www.iviewui.com),各有千秋吧，大家可以根据自己的需要选择

二、为什么需要安装

　　最简单是一种，直接下载并用 <script> 标签引入，Vue 就会被注册为一个全局变量。但是推荐构建大型应用时推荐使用 NPM 安装， NPM 能很好地和诸如Webpack或Browserify模块打包器配合使用

三、开发环境

　　1.Node.js: javascript运行环境(runtime)；

　　2.npm: Nodejs下的包管理器。由于国内使用npm会很慢,这里推荐使用淘宝NPM镜像（http://npm.taobao.org/）

　　3.webpack: 它主要的用途是通过 CommonJS 的语法把所有浏览器端需要发布的静态资源做相应的准备，比如资源的合并和打包。

　　4.vue-cli: Vue-cli是Vue的脚手架工具，主要作用：目录结构、本地调试、代码部署、热加载、单元测试

四、安装Node

　　1.从node.js官网下载并安装node(吐槽下，下载了好多遍页面下载好，就用了之前的版本)

　　

　　win+R，输入cmd，接着输入node -v检测是否安装成功。

　　

五、安装npm的国内镜像---cnpm

　　在命令行中输入npm install -g cnpm --registry=http://registry.npm.taobao.org

　　

　　入上图，安装完成。

六、安装vue-cli脚手架构建工具

　　在命令行中运行命令cnpm install -g vue-cli 安装完成。

　　

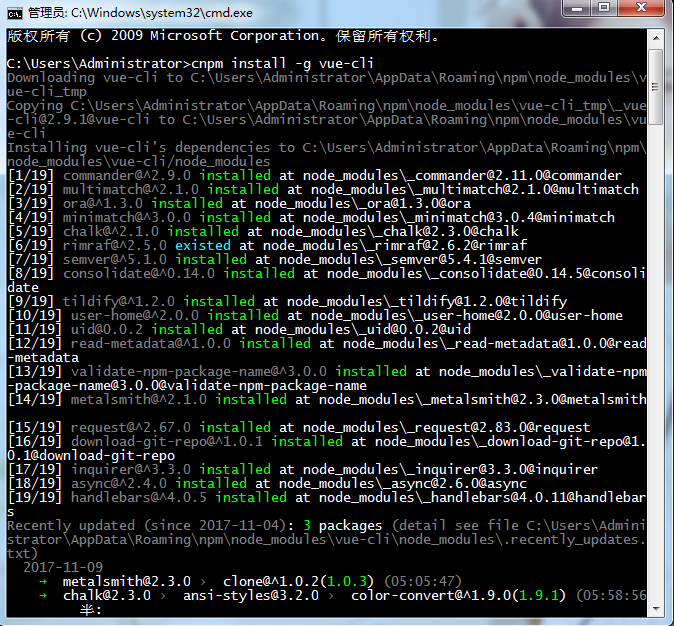
　　以上，我们需要准备的环境和工具都准备好了，接下来就开始使用vue-cli来构建项目。

七、用vue-cli构建我们的第一个项目

　　首选要选择项目目录 暂时放到桌面。cd desktop

　　然后运行命令vue init webpack MyVue这个命令的意思是初始化一个项目，其中webpack是构建工具

　　再然后就是编写项目名称，描述，作者等信息等（注意：User EsLint to lint to your code,这个要选NO,该选项为使用ESLint规范你的代码，一个空格错误都将报错，暂时不开启，可以避免不必要的麻烦）

　　

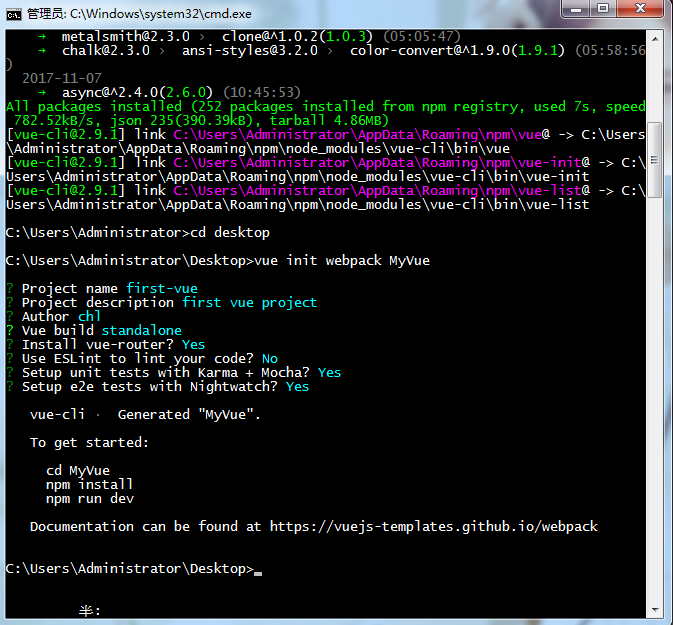
　　此时，我们桌面上就有了项目文件夹

　　

　　嗯，结束了么？No! 还得安装依赖包

　　

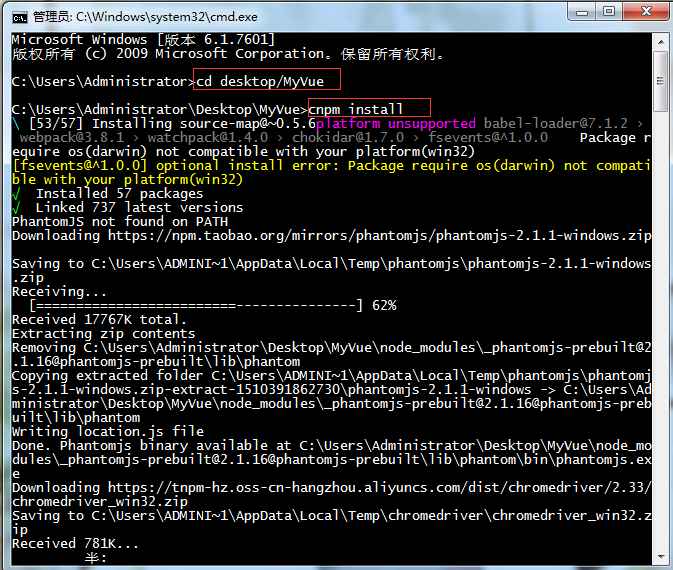
　　安装完依赖包之后，就可以运行整个项目了.

八、运行项目

　　在项目目录下运行使用npm run dev，便可以打开本地服务器实时查看效果（localhost:8080）

　　

　　

　　这样，整个安装步骤就基本结束了，其实还是很繁琐的，查找了网上很多资料。后面会开始我们vue正式的学习篇章……