AcWing 1248. 灵能传输 蓝桥杯

蓝桥杯的一道题：灵能传输 https://www.acwing.com/problem/content/description/1250/

首先是简化操作，将原数组转化为前缀和数组（下标都是从1开始），一次灵能传输对原数组涉及三个数（a[i-1],a[i],a[i+1]）的操作，而且操作比较麻烦，但是如果转化成前缀和数组后等价于(s[i-1]与s[i])交换位置。

原来的目标是求a[i]绝对值最小值，那么现在的目标变为求s[i]-s[i-1]的绝对值最大值，其中设计的数有s[0~n]

2.由于对数组可以任意交换位置，经过简单的思考可以得知如果序列单调（后面就说成单增了），那么即为所求，那么对s数组排序即可。

但是存在一个问题，即s[0],s[n]参与最后求s[i]-s[i-1]的绝对值最大值的计算，但是由于题意可知s[0],s[n]是无法移动的，因此在此情况下怎么排序呢？

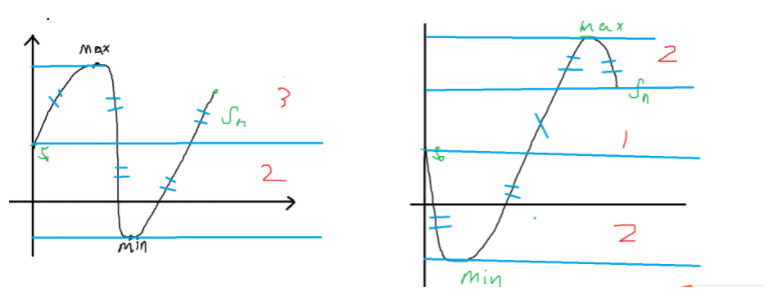
上面两种方式（这里假设s0 是小于sn的（如果是大于，swap一下就是一样的））

右边更优秀，为何？

简单理解就是由于s0比sn更小，因此左边s0到最大值比右边sn到最大值明显差值会小一些。

现在问题变为如何排成右边这种序列？

答案以代码呈现：

if(s0 > sn) swap(s0, sn);

        sort(s, s + n + 1);

        for(int i = 0; i <= n; i ++ )
            if(s[i] == s0)
            {
                s0 = i;
                break;
            }

        for(int i = n; i >= 0; i -- )
            if(s[i] == sn)
            {
                sn = i;
                break;
            }

        memset(st, 0,sizeof st);
        int l = 0 ,r = n;

        for(int i = s0; i >= 0; i -= 2)
        {
            a[l ++ ] = s[i];
            st[i] = true;
        }

        for(int i = sn; i <= n; i += 2)
        {
            a[r -- ] = s[i];
            st[i] = true;
        }

        for(int i = 0; i <= n; i ++ )
            if(!st[i]) a[l ++ ] = s[i];

        LL res = 0;

        for(int i = 1; i <= n; i ++ ) res = max(res, abs(a[i] - a[i - 1]));

核心就是隔一个一取，为何是隔一个，反证法想一想不隔，或者隔两个是个什么情况（反过来的时候是隔两个，就比一次隔一个反过来也是隔一个大了）可以参见y总视频。

详细分析见：

• [y总视频，17分钟之后](AcWing 1248. 灵能传输（蓝桥杯C++ AB组辅导课） - AcWing)
• AcWing 1248. 灵能传输--详细说一些细节 - AcWing
• AcWing 1248. 灵能传输 - AcWing

java代码实现：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

/**
 *
 */
public class Main {
    static int N=300000+5;
    //细节：由于涉及前缀和再加上数据范围，因此需要long
    static long[] a=new long[N];
    static long[] sum=new long[N];
    static int n;
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        String[] line = reader.readLine().split(" ");
        int t=Integer.parseInt(line[0]);
        while (t--!=0) {
            Arrays.fill(a, 0);
            Arrays.fill(sum, 0);
            line=reader.readLine().split(" ");
            n=Integer.parseInt(line[0]);
            line=reader.readLine().split(" ");
            for (int i = 1; i <= n; i++) {
                a[i]=Integer.parseInt(line[i-1]);
            }
            start();
        }

    }
    private static void start() {
        for (int i = 1; i <= n; i++) {
            sum[i]=sum[i-1]+a[i];
        }
        //s0开始是记数，后面就是记下标了
        long s0=sum[0],sn=sum[n];
        if (s0>sn) {
            long t=s0;
            s0=sn;
            sn=t;
        }
        Arrays.sort(sum,0,n+1);
        for (int i = 0; i <= n; i++) {
            if (sum[i]==s0) {
                s0=i;
                //第一次遇到就break，否则赋值之后万一又意外相等了
                break;
            }
        }
        for (int i = n; i >= 0; i--) {
            if (sum[i]==sn) {
                sn=i;
                break;
            }
        }
        boolean[] st=new boolean[N];
        int l=0,r=n;
        //a[i]在计算前缀和之后就没有使用了，因此这里再次使用a来减小数据空间
        //跳着读取
        for (int i = (int)s0; i >= 0; i-=2) {
            a[l++]=sum[i];
            st[i]=true;
        }
        for(int i=(int)sn;i<=n;i+=2){
            a[r--]=sum[i];
            st[i]=true;
        }
        for (int i = 0; i <= n; i++) {
            if (!st[i]) {
                a[l++]=sum[i];
            }
        }

        long res=0L;
        for (int i = 1; i <= n; i++) {
            res=Math.max(res,Math.abs( a[i]-a[i-1]));
        }
        System.out.println(res);
    }
}