MATLAB进行无约束优化
首先先给出三个例子引入fminbnd和fminuc函数求解无约束优化,对这些函数有个初步的了解
求f=2exp(-x)sin(x)在(0,8)上的最大、最小值。

例2 边长3m的正方形铁板,四角减去相等正方形,制成方形无盖水槽。怎样减使水槽容积最大。
解:列出目标函数(加负号,转化为求最小)
min y=-((3-2x)^2)*x

例3 求多元函数最小值
minf(x)=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1)
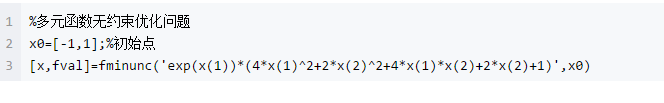
下面是MATLAB优化工具箱的主要功能






MATLAB进行无约束优化的更多相关文章
- 02(c)多元无约束优化问题-牛顿法
此部分内容接<02(a)多元无约束优化问题>! 第二类:牛顿法(Newton method) \[f({{\mathbf{x}}_{k}}+\mathbf{\delta })\text{ ...
- 02(a)多元无约束优化问题
2.1 基本优化问题 $\operatorname{minimize}\text{ }f(x)\text{ for }x\in {{R}^{n}}$ 解决无约束优化问题的一般步骤 ...
- 无约束优化方法(梯度法-牛顿法-BFGS- L-BFGS)
本文讲解的是无约束优化中几个常见的基于梯度的方法,主要有梯度下降与牛顿方法.BFGS 与 L-BFGS 算法. 梯度下降法是基于目标函数梯度的,算法的收敛速度是线性的,并且当问题是病态时或者问题规模较 ...
- 02(b)多元无约束优化问题-最速下降法
此部分内容接02(a)多元无约束优化问题的内容! 第一类:最速下降法(Steepest descent method) \[f({{\mathbf{x}}_{k}}+\mathbf{\delta }) ...
- 01(b)无约束优化(准备知识)
1.解方程转化为优化问题 $n\left\{ \begin{aligned}& {{P}_{1}}(x)=0 \\ & {{P}_{2}}(x)=0 \\ & \text{ ...
- 02(d)多元无约束优化问题-拟牛顿法
此部分内容接<02(a)多元无约束优化问题-牛顿法>!!! 第三类:拟牛顿法(Quasi-Newton methods) 拟牛顿法的下降方向写为: ${{\mathbf{d}}_{k}}= ...
- 02(e)多元无约束优化问题- 梯度的两种求解方法以及有约束转化为无约束问题
2.1 求解梯度的两种方法 以$f(x,y)={{x}^{2}}+{{y}^{3}}$为例,很容易得到: $\nabla f=\left[ \begin{aligned}& \frac{\pa ...
- 无约束优化算法——牛顿法与拟牛顿法(DFP,BFGS,LBFGS)
简介:最近在看逻辑回归算法,在算法构建模型的过程中需要对参数进行求解,采用的方法有梯度下降法和无约束项优化算法.之前对无约束项优化算法并不是很了解,于是在学习逻辑回归之前,先对无约束项优化算法中经典的 ...
- ubuntu下matlab的无界面启动---命令行操作
命令行下运行 Matlab 及 函数 首先参考命令行下matlab的运行参数的定义与作用:http://www.cnblogs.com/beanocean/p/3677404.html 创建示例程序: ...
随机推荐
- MATLAB卷积运算(conv、conv2)解释
来源:https://www.cnblogs.com/hyb221512/p/9276621.html 1.conv(向量卷积运算) 所谓两个向量卷积,说白了就是多项式乘法.比如:p=[1 2 3], ...
- Android 布局文件
<LinearLayout xmlns:android="http://schemas.android.com/apk/res/android" xmlns:tools=&q ...
- Delphi操作XML - 冰雪傲骨
Delphi操作XMl,只要使用 NativeXml.我是用的版本是4..NativeXML的使用方法比较简单,但是功能很强大. XE2的话,要在simdesign.inc后面加上: // Delph ...
- 【Selenium】Option加载用户配置,Chrom命令行参数
about:version - 显示当前版本 about:memory - 显示本机浏览器内存使用状况 about:plugins - 显示已安装插件 about:histograms - 显示历史记 ...
- codeforces 655D D. Robot Rapping Results Report(拓扑排序+拓扑序记录)
题目链接: D. Robot Rapping Results Report time limit per test 2 seconds memory limit per test 256 megaby ...
- codeforces 631B B. Print Check
B. Print Check time limit per test 1 second memory limit per test 256 megabytes input standard input ...
- python中的单引号,双引号和三双引号的区别
1.单引号和双引号没有区别.都可以用就是为了方便,减少写太多的转义字符. 比如: str='Let\'s go!' str="Let's go!" 两种等价,但是第二种写法显然更优 ...
- git克隆某一个branch
git clone -b <branch> <remote_repo> 例如: git clone -b 指定的分支名字
- ffmpeg用法(心得体会还有你见过的用法)
ffmpeg的常用用法很多,我这里提供的用法有可能有许多地方是你没见过的. 一.ffmpeg合并视频 我经常需要切割再把一些零碎的视频给拼接起来,这样可以省许多磁盘空间.其实用mencoder挺不错的 ...
- bzoj 4822~4824 CQOI2017题解
老C的任务 题目大意: 维护一个二维平面,初始给出一些点及其权.多次询问某个矩形内的权和. n,m <= 100000 题解: 签到题. CDQ水一水. #include <cstdio& ...
