机器学习-线性分类-支持向量机SVM-SMO算法代码实现-15

1. alpha2 的修剪

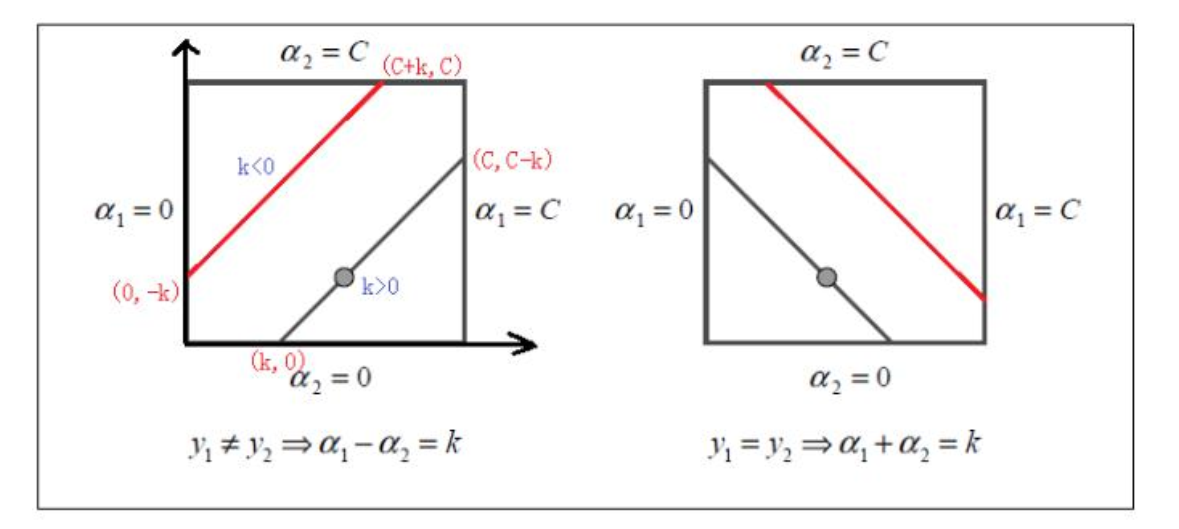
if y1 != y2 :

α1 - α2 = k # 不用算k的具体大小

if k > 0: # 上图的左 下这条线

α2 的区间 (0, c-k)

k < 0 : # 上图的左 下这条线

α2 的区间 （-k, C）

所以：

L = max(0, -k) # k>0 还是<0 都统一表达了

H = min(c, c-k)

else:

y1 = y2 右边的图 同理

2.参考

参考：https://zhuanlan.zhihu.com/p/49331510



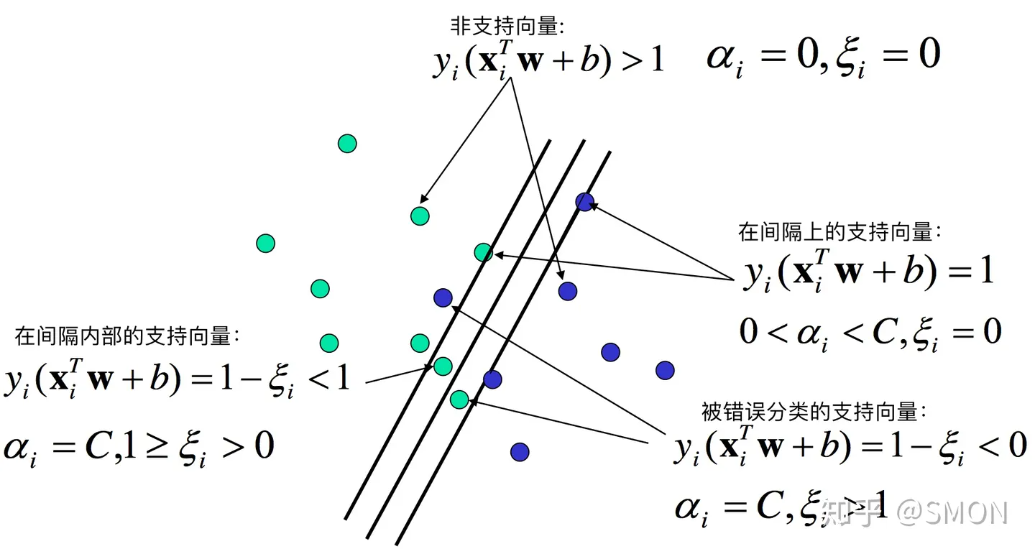
非支撑向量：

alpha=0

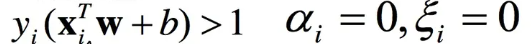
间隔上的支撑向量：

0<alpha<c

间隔之内：

alpha=c and 0< ei <1

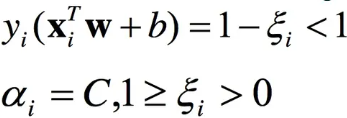
上面的三种都是正确分类的；

错误分类的：



alpha=c and ei > 1

yi(wxi+b) = 1-ei < 0 使负的 预测的与实际的符号相反

3. 代码实现

"""
算法思想：
创建一个alpha向量 并初始化为0

当迭代次数小于 最大迭代次数（外层循环）：
    遍历α中的每一个αi（内层循环）：
        如果该αi可以被优化：
            随机选择另一个αj
            同时优化 αi aj
            如果αi aj优化完毕退出内层循环
"""
import numpy
import numpy as np
import random
import matplotlib.pyplot as plt

def load_data(filename):
    X = []
    y = []

    fr = open(filename)

    for line in fr.readlines():
        x1, x2, y_true = line.strip().split("\t")
        X.append([float(x1), float(x2)])
        y.append(float(y_true))
    fr.close()
    return numpy.array(X), np.array(y)

def show_data(filename, line=None):
    X, y = load_data("./testSet.txt")
    class_1_index = np.where(y == -1)  # -1 负样本的索引
    X_class_1 = X[class_1_index, :].reshape(-1, 2)  # 负样本对应的X取出

    class_2_index = np.where(y == 1)  # +1 正样本的索引
    X_class_2 = X[class_2_index, :].reshape(-1, 2)  # 正样本对应的X取出

    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)

    ax.scatter(X_class_1[:, 0], X_class_1[:, 1], c="r", label="$-1$")
    ax.scatter(X_class_2[:, 0], X_class_2[:, 1], c="g", label="$+1$")

    plt.legend()

    if line is not None:
        alphas, b = line
        x = np.linspace(1, 8, 50)
        w = np.sum(alphas*y[:, np.newaxis]*X, axis=0)
        # w1*x1 + w2*x2 +b = 0    # 或者 +1  -1
        y = np.array([(-b - w[0]*x[i]) / w[1]for i in range(50)])
        y1 = np.array([(1 -b - w[0]*x[i]) / w[1]for i in range(50)])
        y2 = np.array([(-1 -b - w[0]*x[i]) / w[1]for i in range(50)])
        ax.plot(x, y, "b-")
        ax.plot(x, y1, "b--")
        ax.plot(x, y2, "b--")

    plt.show()

def smo_simple(dataArr, yArr, C, toler, maxIter):
    numSample, numDim = dataArr.shape  # 100行 2列

    # 初始化
    b = 0
    alphas = np.zeros((numSample, 1))

    iterations = 0  # 迭代次数

    while iterations < maxIter:

        alphaPairsChanged = 0

        for i in range(numSample):
            # 针对对i个样本给出预测值 这里没有使用核函数变换
            # fXi= wXi+b
            # alphas * y * X * Xi +b   Xi为一条样本
            fXi = np.sum(alphas * yArr[:, np.newaxis] * dataArr * dataArr[i, :]) + b

            # Ei 为误差
            Ei = fXi - yArr[i]
            """
            kkt 约束条件：
            yi*(wXi+b) >= 1 且alpha=0  远离边界 正常分类的 ----条件1
            yi*(wXi+b) = 1 且0<alpha<c 边界上面
            yi*(wXi+b) < 1 且 alpha=c 两条边界之间  ----条件2

            # 0 <= alphas[i] <= C 已经在边界上的 alpha不能再优化

            Ei = fXi - yArr[i] 两边都 乘以 yArr[i]
            yArr[i]*Ei = yArr[i]*fXi - 1  # 偏差
            如果 yArr[i]*Ei < -toler alpha应该为C 如果<C 就需要优化  ----对应条件2
            如果 yArr[i]*Ei > toler  alpha应该为0 如果>0 就需要优化  ----对应条件1

            """

            if (   (yArr[i]*Ei < -toler) and  (alphas[i] < C)  ) or ( (yArr[i]*Ei > toler) and (alphas[i] > 0)):
                # 进入这里 说明需要优化alpha[i] 我们在随机取一条alpha[j]     j!=i
                j = selectJrand(i, numSample)

                fXj = np.sum(alphas * yArr[:, np.newaxis] * dataArr * dataArr[j, :]) + b
                Ej = fXj - yArr[j]

                # 先复制一份old alphaI  alphaJ
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()

                # 根据 yArr[i]  yArr[j] 是否同号 计算 L H
                if yArr[i] != yArr[j]:
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L == H:
                    print("L == H")
                    continue

                # 计算 eta, eta是alpha[j]的最大修正量 eta == 0 则 continue
                # eta = K(1,1)+K(2,2) - 2K(1,2)
                eta = (np.sum(dataArr[i,:] * dataArr[i, :]) +
                       np.sum(dataArr[j, :] * dataArr[j, :]) -
                       2 * np.sum(dataArr[i,:] * dataArr[j, :]))

                if eta == 0:
                    continue

                # 计算新的alphas[j]
                alphas[j] = alphaJold + yArr[j]*(Ei - Ej) / eta

                # 修剪新的alphas[j]
                alphas[j] = clipAlpha(alphas[j], H, L)

                # 新的alphas[j] 与 alphaJold 如果改动量很小 则 contine 退出
                if abs(alphaJold - alphas[j]) < 0.00001:
                    continue

                # 更新 alphas[i]
                alphas[i] = alphaIold + yArr[i] * yArr[j] * (alphaJold - alphas[j])

                # 计算参数b
                bi = b - Ei - yArr[i] * (alphas[i] - alphaIold) * np.sum(dataArr[i, :] * dataArr[i, :]) - \
                     yArr[j] * (alphas[j] - alphaJold) * np.sum(dataArr[i, :] * dataArr[j, :])
                bj = b - Ej - yArr[i] * (alphas[i] - alphaIold) * np.sum(dataArr[i, :] * dataArr[j, :]) - \
                     yArr[j] * (alphas[j] - alphaJold) * np.sum(dataArr[j, :] * dataArr[j, :])

                if 0<alphas[i]<C:
                    b = bi
                elif 0<alphas[j]<C:
                    b = bj
                else:
                    b = (bi+bj)/2

                # 走到这里说明 alpha b 更新了
                alphaPairsChanged += 1

                # 输出
                print(f"iter: {iterations}, i: {i}, pairs changed: {alphaPairsChanged}")
        if alphaPairsChanged ==0:
            iterations += 1
        else:
            iterations =0
    return b, alphas

def selectJrand(i, numSample):
    j = i
    while j == i:
        j = int(random.uniform(0, numSample))

    return j

def clipAlpha(aj, H, L):
    if aj > H:
        return H
    if aj < L:
        return L
    return aj

if __name__ == '__main__':
    X, y = load_data("./testSet.txt")
    C = 0.6
    toler = 0.001
    maxIter = 40
    b, alphas = smo_simple(X, y, C, toler, maxIter)
    print(b)
    print(alphas)
    show_data("./testSet.txt", line=(alphas, b))

4. 优缺点

任何算法都有其优缺点，支持向量机也不例外。

支持向量机的优点是:

由于SVM是一个凸优化问题，所以求得的解一定是全局最优而不是局部最优。

不仅适用于线性线性问题还适用于非线性问题(用核技巧)。

拥有高维样本空间的数据也能用SVM，这是因为数据集的复杂度只取决于支持向量而不是数据集的维度，这在某种意义上避免了“维数灾难”。

理论基础比较完善(例如神经网络就更像一个黑盒子)。

支持向量机的缺点是:

二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)

只适用于二分类问题。(SVM的推广SVR也适用于回归问题；可以通过多个SVM的组合来解决多分类问题