[Bayes] Why we prefer Gaussian Distribution
最后还是选取一个朴素直接的名字,在此通过手算体会高斯的便捷和神奇。
Ref: The Matrix Cookbook
注意,这里的所有变量默认都为多元变量,不是向量就是矩阵。多元高斯密度函数如下:

高斯的线性组合结果y还是高斯
期望答案很直接。

方差需要计算,注意其中的矩阵计算技巧,要记下来。

高斯相乘还是高斯

如下计算用到了8.1.8。这里的tricky是:8.1.8之后得到的结果虽然复杂,但
我们想尽办法做出z的分布,就是为了在之后的积分中直接干掉z,也便留下了我们需要的p(x)。
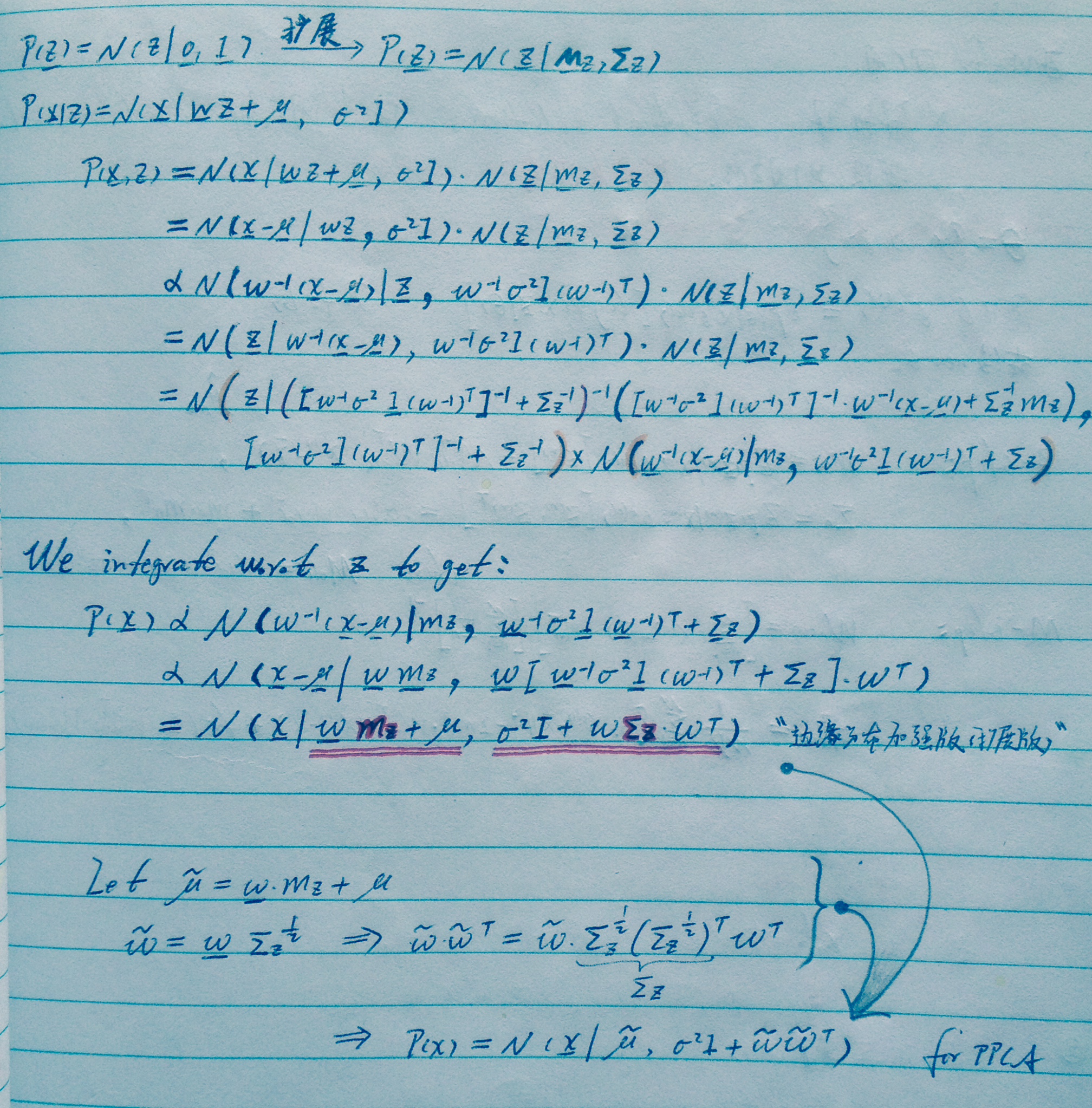
[Bayes] Why we prefer Gaussian Distribution的更多相关文章
- 一起啃PRML - 1.2.4 The Gaussian distribution 高斯分布 正态分布
一起啃PRML - 1.2.4 The Gaussian distribution 高斯分布 正态分布 @copyright 转载请注明出处 http://www.cnblogs.com/chxer/ ...
- 正态分布(Normal distribution)又名高斯分布(Gaussian distribution)
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学.物理及project等领域都很重要的概率分布,在统计学的很多方面有着重大的影 ...
- UNDERSTANDING THE GAUSSIAN DISTRIBUTION
UNDERSTANDING THE GAUSSIAN DISTRIBUTION Randomness is so present in our reality that we are used to ...
- 高斯分布(Gaussian Distribution)的概率密度函数(probability density function)
高斯分布(Gaussian Distribution)的概率密度函数(probability density function) 对应于numpy中: numpy.random.normal(loc= ...
- 广义逆高斯分布(Generalized Inverse Gaussian Distribution)及修正贝塞尔函数
1. PDF generalized inverse Gaussian distribution (GIG) 是一个三参数的连续型概率分布: f(x)=(a/b)p/22Kp(ab−−√)xp−1e− ...
- 【翻译】拟合与高斯分布 [Curve fitting and the Gaussian distribution]
参考与前言 英文原版 Original English Version:https://fabiandablander.com/r/Curve-Fitting-Gaussian.html 如何通俗易懂 ...
- 吴恩达机器学习笔记56-多元高斯分布及其在误差检测中的应用(Multivariate Gaussian Distribution & Anomaly Detection using the Multivariate Gaussian Distribution)
一.多元高斯分布简介 假使我们有两个相关的特征,而且这两个特征的值域范围比较宽,这种情况下,一般的高斯分布模型可能不能很好地识别异常数据.其原因在于,一般的高斯分布模型尝试的是去同时抓住两个特征的偏差 ...
- 吴恩达机器学习笔记53-高斯分布的算法(Algorithm of Gaussian Distribution)
如何应用高斯分布开发异常检测算法呢? 异常检测算法: 对于给定的数据集
- 吴恩达机器学习笔记52-异常检测的问题动机与高斯分布(Problem Motivation of Anomaly Detection& Gaussian Distribution)
一.问题动机 异常检测(Anomaly detection)问题是机器学习算法的一个常见应用.这种算法的一个有趣之处在于:它虽然主要用于非监督学习问题,但从某些角度看,它又类似于一些监督学习问题. 给 ...
随机推荐
- python --- json模块和pickle模块详解
json:JSON(JavaScript Object Notation, JS 对象标记) 是一种轻量级的数据交换格式(用于数据序列化和反序列化).(适用于多种编程语言,可以与其他编程语言做数据交换 ...
- Java历程-初学篇 Day04选择结构(1)
一,if 1,单分支 if(条件){ } 示例: 2,双分支 if(条件){ }else{ } 示例: 3,多重if if(条件){ }else if(条件){ }else{ } 示例: 4,嵌套if ...
- python 多进程间交换信息与共享信息
多线程调用函数,获取其返回值,个人总结了三种方法: 一.Queue(进程队列) 构造方法:multiprocessing.Queue([maxsize]) Queue.Queue类即是一个队列的同步实 ...
- DataGridView一些常用操作
SqlConnection conn = new SqlConnection('Server=(local);DataBase=test;User=sa;Pwd=sa'); SqlDataAdapte ...
- 原生API实现拖拽上传文件实践
功能: 拖拽上传文件.图片,上传的进度条,能够同时上传多个文件. 完整的demo地址:https://github.com/qcer/FE-Components/tree/master/QDrag 涉 ...
- iOS开发工程师必备技能(持续更新)
Objective-C Objective-C语言基础 library,framework的制作 Runtime 编程 LLVM 原理和调优 操作系统 iOS内存管理和调优 iOS的文件系统和沙盒机制 ...
- JavaScript之“创意时钟”项目
“时钟展示项目”说明文档(文档尾部附有相应代码) 一.最终效果展示: 二.项目亮点 1.代码结构清晰明了 2.可以实时动态显示当前时间与当前日期 3.界面简洁.美观.大方 4.提高浏览器兼容性 三.知 ...
- HTML之事件处理程序
HTML事件 <body> <input type="button" value="按钮1" id="but1" oncl ...
- MySQL技术内幕汇总
MySql技术内幕之MySQL入门(1) MySql技术内幕之MySQL入门(1) 检查系统中是否已经安装了MySQL sudo netstat -tap | grep mysql 若没有显示已安装结 ...
- MongoDB查询分析
MongoDB 查询分析可以确保我们建立的索引是否有效,是查询语句性能分析的重要工具.MongoDB 查询分析常用函数有:explain() 和 hint(). 1. explain(): 提供查询信 ...
