Selenium+Python自动化测试学习问题总结笔记
1.问题描述:不能导入自定义类
错误内容:This inspection detects names that should resolve but don't. Due to dynamic dispatch and duck typing, this is possible in a limited but useful number of cases. Top-level and class-level items are supported better than instance items
截图:(count.py文件不能导入在相同路径下的pub.py的方法)

解决方法1:将导入部分写成:from WebTest.project.pub import add (将路径明确写入)
解决方法2:进入:File—setting—Bulidout,Excution,Deployment—Console—Python Console 如下图操作
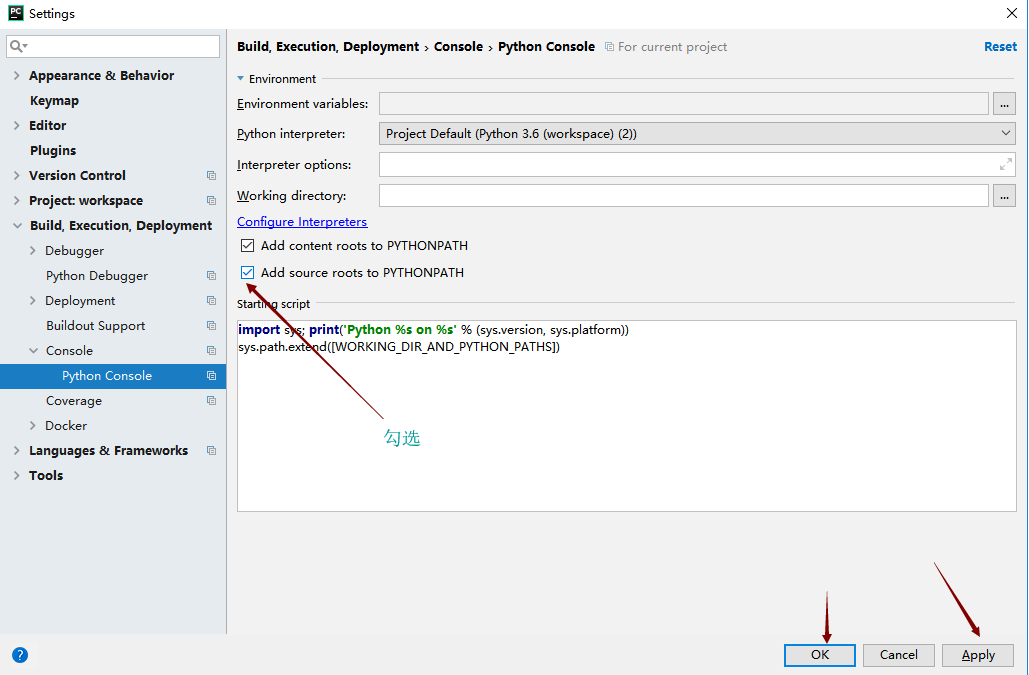
之后右击项目,如下图操作
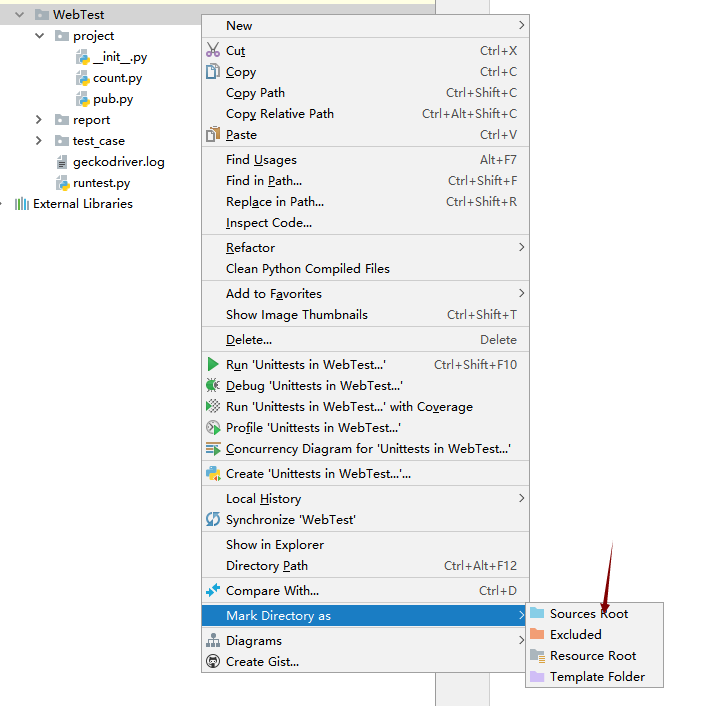
Selenium+Python自动化测试学习问题总结笔记的更多相关文章
- selenium + python自动化测试unittest框架学习(五)webdriver的二次封装
因为webdriver的api方法很长,再加上大多数的定位方式是以xpath方式定位,更加让代码看起来超级长,为了使整体的代码看起来整洁,对webdriver进行封装,学习资料来源于虫师的<se ...
- selenium + python自动化测试unittest框架学习(二)
1.unittest单元测试框架文件结构 unittest是python单元测试框架之一,unittest测试框架的主要文件结构: File >report >all_case.py &g ...
- selenium + python 自动化测试环境搭建
selenium + python 自动化测试 —— 环境搭建 关于 selenium Selenium 是一个用于Web应用程序测试的工具.Selenium测试直接运行在浏览器中,就像真正的用户在操 ...
- selenium+python自动化测试
F12: 右键 选择复制 path 在selenium+python自动化测试(一)–环境搭建中,运行了一个测试脚本,脚本内容如下: from selenium import webdriver ...
- selenium + python自动化测试unittest框架学习(一)selenium原理及应用
unittest框架的学习得益于虫师的<selenium+python自动化实践>这一书,该书讲得很详细,大家可以去看下,我也只学到一点点用于工作中,闲暇时记录下自己所学才能更加印象深刻. ...
- Selenium 与自动化测试 —— 《Selenium 2 自动化测试实战》读书笔记
背景 最近在弄 appium,然后顺便发现了 Selenium 框架和这本书,恰好这本书也介绍了一些软件测试&自动化测试的理论知识,遂拿过来学习学习.所以本文几乎没有实践内容,大多都是概念和工 ...
- selenium+python自动化测试系列(一):登录
最近接手商城的项目,针对后台测试,功能比较简单,但是流程比较繁多,涉及到前后台的交叉测试.在对整个项目进行第一轮测试完成之后,考虑以后回归测试任务比较重,为了减轻回归测试的工作量,所以考虑后台 ...
- 《自拍教程5》Python自动化测试学习思路
前提:熟悉测试业务及流程 任何Python自动化测试的前提,都是必须先熟悉实际测试业务. 任何脱离实际测试业务的自动化都是噱头且无实际意义! 测试的基本流程基本是: 测试需求分析,测试用例设计与评审, ...
- selenium + python自动化测试环境搭建
selenium的在python平台的搭建: 搭建平台windows 准备工具如下: --------------------------------------------------------- ...
随机推荐
- PHP SPL神器实现堆排序
之前学习过内部排序的八大算法,也一一写过代码实现.其中堆排序的原理是 将一颗二叉树初始化为堆 依次将最后一个结点与堆顶结点交换.然后调整堆顶元素位置,重置堆. 将二叉树初始化为堆可以看做从最后一个非叶 ...
- postGresql关键字字段重名
在postGresql中如果关键字和自定义的字段重名 即使使用[ ](中括号)或者 ' '(单引号)都没有用,经本人实验. 如果使用" "(双引号),则可以.
- Java8新特性 -- 四大内置的核心函数式接口
可以把这些函数式接口作为方法的参数. 1.0 核心内置函数式接口一: 消费型接口@FunctionalInterfacepublic interface Consumer<T> { voi ...
- 函数的类型:函数也是类型 (*)->*
函数的类型:函数也是类型 (*)->* 函数类型作为类型可以定义变量,使得函数变量具有可替代性,这个是高阶函数的编程基础. 使用函数的类型可以定义函数的变量,并用函数给这个变量赋值: 每一个函数 ...
- 1084. [SCOI2005]最大子矩阵【网格DP】
Description 这里有一个n*m的矩阵,请你选出其中k个子矩阵,使得这个k个子矩阵分值之和最大.注意:选出的k个子矩阵 不能相互重叠. Input 第一行为n,m,k(1≤n≤100,1≤m≤ ...
- 【[SDOI2017]数字表格】
求 \[Ans=\prod_{i=1}^N\prod_{j=1}^MFib[(i,j)]\] 连乘的反演,其实并没有什么不一样 我们把套路柿子拿出来 \[F(n)=\sum_{i=1}^N\sum_{ ...
- [SCOI2007]组队
嘟嘟嘟 这题有人说部分分O(n3)暴力,然而我暴力都没写过,调了半天也没用……还是看题解吧 首先,咱把A * ( h – minH ) + B * ( s – minS ) <= C 变个型,得 ...
- virtualbox+vagrant学习-2(command cli)-8-vagrant Package命令
Package 格式: vagrant package [options] [name|id] 这将当前正在运行的VirtualBox或Hyper-V环境打包到一个可重用的box中.如果provide ...
- css自问自答(一)
css自问自答(一) 1.块级元素和行内元素特性与区别? 块级:display:block <div>.<p>.<h1>...<h6>.<ol&g ...
- java学习笔记-JavaWeb篇三
63 JSTL_表达式操作64 JSTL_流程控制操作 65 JSTL_迭代操作 66 JSTL_URL操作67 JSTL_改写MVC案例68 Filter概述 69 创建HttpFilter 70 ...
