最短路径——SPFA算法

一、前提引入

我们学过了Bellman-Ford算法，现在又要提出这个SPFA算法，为什么呢？

考虑一个随机图（点和边随机生成），除了已确定最短路的顶点与尚未确定最短路的顶点之间的边，其它的边所做的都是无用的，大致描述为下图（分割线以左为已确定最短路的顶点）：

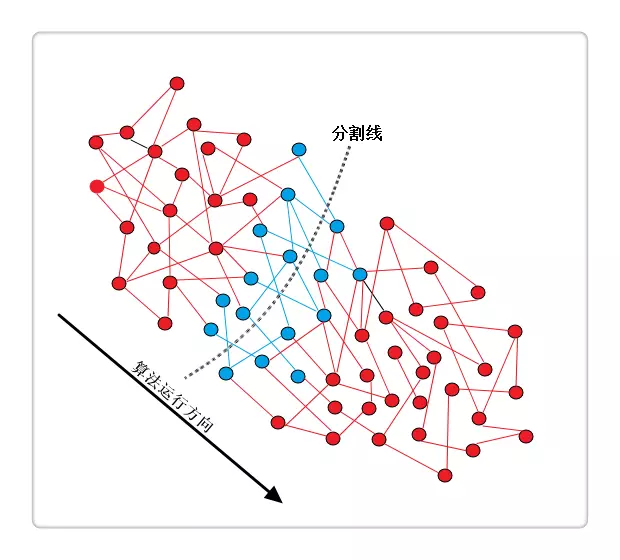
其中红色部分为所做无用的边，蓝色部分为实际有用的边。既然只需用到中间蓝色部分的边，那就是SPFA算法的优势之处了。

二、算法描述

算法特点：在 Bellman-ford 算法的基础上加上一个队列优化，减少了冗余的松弛操作，是一种高效的最短路算法。

时间复杂度：O（mn）

关键词：初始化    松弛操作    队列

主要变量如下：

int n　　　           表示有n个点，从1~n标号

int s,t 　　　        s为源点，t为终点

int dis[N]　          dis[i]表示源点s到点i的最短路径

int pre[N]　         记录路径，pre[i]表示i的前驱结点

bool vis[N]          vis[i]=true表示点i在队列中

queue<int> q     队列，在整个算法中有顶点入队了要记得标记vis数组，有顶点出队了记得消除那个标记

【初始化】

dis数组全部赋值为INF，pre数组全部赋值为-1（表示还不知道前驱），

dis[s] = 0 表示源点不要求最短路径（或者最短路径就是0）。

【队列+松弛操作】

读取队头顶点u，并将队头顶点u出队（记得消除标记）；将与点u相连的所有点v进行松弛操作，如果能更新估计值（即令d[v]变小），那么就更新，另外，如果点v没有在队列中，那么要将点v入队（记得标记），如果已经在队列中了，那么就不用入队，这样不断从队列中取出顶点来进行松弛操作。

以此循环，直到队空为止就完成了单源最短路的求解。

【算法过程】

设立一个队列用来保存待优化的顶点，优化时每次取出队首顶点 u，并且用 u 点当前的最短路径估计值dis[u]对与 u 点邻接的顶点 v 进行松弛操作，如果 v 点的最短路径估计值dis[v]可以更小，且 v 点不在当前的队列中，就将 v 点放入队尾。这样不断从队列中取出顶点来进行松弛操作，直至队列空为止。

【检测负权回路】

方法：如果某个点进入队列的次数大于等于 n，则存在负权回路，其中 n 为图的顶点数。

说明：SPFA无法处理带负环的图。

三、代码实现

#include<iostream>
#include<queue>
#include<stack>
using namespace std;

int matrix[100][100];  //邻接矩阵
bool visited[100];     //标记数组
int dist[100];         //源点到顶点i的最短距离
int path[100];         //记录最短路的路径
int enqueue_num[100];  //记录入队次数
int vertex_num;        //顶点数
int edge_num;          //边数
int source;            //源点

bool SPFA()
{
    memset(visited, 0, sizeof(visited));
    memset(enqueue_num, 0, sizeof(enqueue_num));
    for (int i = 0; i < vertex_num; i++)
    {
        dist[i] = INT_MAX;
        path[i] = source;
    }

    queue<int> Q;
    Q.push(source);
    dist[source] = 0;
    visited[source] = 1;
    enqueue_num[source]++;
    while (!Q.empty())
    {
        int u = Q.front();
        Q.pop();
        visited[u] = 0;
        for (int v = 0; v < vertex_num; v++)
        {
            if (matrix[u][v] != INT_MAX)  //u与v直接邻接
            {
                if (dist[u] + matrix[u][v] < dist[v])
                {
                    dist[v] = dist[u] + matrix[u][v];
                    path[v] = u;
                    if (!visited[v])
                    {
                        Q.push(v);
                        enqueue_num[v]++;
                        if (enqueue_num[v] >= vertex_num)
                            return false;
                        visited[v] = 1;
                    }
                }
            }
        }
    }
    return true;
}

void Print()
{
    for (int i = 0; i < vertex_num; i++)
    {
        if (i != source)
        {
            int p = i;
            stack<int> s;
            cout << "顶点 " << source << " 到顶点 " << p << " 的最短路径是： ";

            while (source != p)  //路径顺序是逆向的，所以先保存到栈
            {
                s.push(p);
                p = path[p];
            }

            cout << source;
            while (!s.empty())  //依次从栈中取出的才是正序路径
            {
                cout << "--" << s.top();
                s.pop();
            }
            cout << "    最短路径长度是：" << dist[i] << endl;
        }
    }
}

int main()
{

    cout << "请输入图的顶点数，边数，源点：";
    cin >> vertex_num >> edge_num >> source;

    for (int i = 0; i < vertex_num; i++)
        for (int j = 0; j < vertex_num; j++)
            matrix[i][j] = INT_MAX;  //初始化matrix数组

    cout << "请输入" << edge_num << "条边的信息：\n";
    int u, v, w;
    for (int i = 0; i < edge_num; i++)
    {
        cin >> u >> v >> w;
        matrix[u][v] = w;
    }

    if (SPFA())
        Print();
    else
        cout << "Sorry,it have negative circle!\n";

    return 0;
}

运行如下：