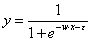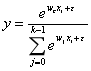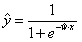机器学习---三种线性算法的比较(线性回归,感知机,逻辑回归)(Machine Learning Linear Regression Perceptron Logistic Regression Comparison)
最小二乘线性回归,感知机,逻辑回归的比较:
|
最小二乘线性回归 Least Squares Linear Regression |
感知机 Perceptron |
二分类逻辑回归 Binary Logistic Regression |
多分类逻辑回归 Multinomial Logistic Regression |
|
|
特征x |
x=([x1,x2,...,xn,1])T |
|||
|
权重w |
w=([w1,w2,...,wn,b])T |
|||
|
目标y |
实数(负无穷大到正无穷大) |
两个类别 1,-1 |
两个类别 0,1 |
多个类别 c=0,1,...,k-1 |
|
目标函数 |
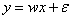 |
 |
(类别1的概率) |
for c=0,1,...,k-1 (全部类别的概率) |
|
对y的估计 |
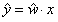 |
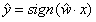 |
(类别1的概率) |
for c=0,1,...,k-1 (全部类别的概率) |
|
映射函数 |
无 |
sign函数 |
sigmoid函数 |
softmax函数 |
|
算法的作用 |
预测连续值(回归) |
预测离散值(分类) |
预测离散值(分类) |
预测离散值(分类) |
|
损失函数 |
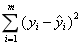 |
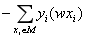 |
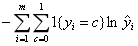 |
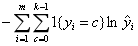 |
|
损失函数的含义 |
观测值与估计值之间的欧式距离平方和 |
错误分类点距离分类超平面的总长度 |
估计的概率分布与真实的概率分布之间的相似程度,对于样本(xi,yi),它的正确分类类别是c,那么如果它计算出的目标属于类别c的分类概率的值为1,则说明分类完全正确,这种情况下对损失函数没有贡献(ln1=0);而如果分类错误,则它计算出的目标属于类别c的的分类概率将是一个小于1的值,这种情况下将对损失函数有所贡献 |
估计的概率分布与真实的概率分布之间的相似程度,对于样本(xi,yi),它的正确分类类别是c,那么如果它计算出的目标属于类别c的分类概率的值为1,则说明分类完全正确,这种情况下对损失函数没有贡献(ln1=0);而如果分类错误,则它计算出的目标属于类别c的的分类概率将是一个小于1的值,这种情况下将对损失函数有所贡献 |
|
损失函数的本质 |
目标y的条件概率P(y|x)在高斯分布下的极大似然估计(取负数和对数) |
/ |
目标y的条件概率P(y|x)在伯努利分布下的极大似然估计(取负数和自然对数) |
目标y的条件概率P(y|x)在多项分布下的极大似然估计(取负数和自然对数) |
|
最优解方法 |
解析解(closed form),梯度下降法,牛顿法,拟牛顿法 |
随机梯度下降法,牛顿法,拟牛顿法 |
梯度下降法,牛顿法,拟牛顿法 |
梯度下降法,牛顿法,拟牛顿法 |
机器学习---三种线性算法的比较(线性回归,感知机,逻辑回归)(Machine Learning Linear Regression Perceptron Logistic Regression Comparison)的更多相关文章
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
原文:http://blog.csdn.net/abcjennifer/article/details/7716281 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- FIFO、LRU、OPT这三种置换算法的缺页次数
考虑下述页面走向: 1,2,3,4,2,1,5,6,2,1,2,3,7,6,3,2,1,2,3,6 当内存块数量分别为3时,试问FIFO.LRU.OPT这三种置换算法的缺页次数各是多少? 答:缺页定义 ...
- 排序—时间复杂度为O(n2)的三种排序算法
1 如何评价.分析一个排序算法? 很多语言.数据库都已经封装了关于排序算法的实现代码.所以我们学习排序算法目的更多的不是为了去实现这些代码,而是灵活的应用这些算法和解决更为复杂的问题,所以更重要的是学 ...
- 基于C#程序设计语言的三种组合算法
目录 基于C#程序设计语言的三种组合算法 1. 总体思路 1.1 前言 1.2 算法思路 1.3 算法需要注意的点 2. 三种组合算法 2.1 普通组合算法 2.2 与自身进行组合的组合算法 2.3 ...
- 网络中,FIFO、LRU、OPT这三种置换算法的缺页次数
FIFO.LRU.OPT这三种置换算法的缺页次数 转载 由于要考计算机四级网络,这里遇到了问题,就搜了一些资料来解疑. 考虑下述页面走向: 1,2,3,4,2,1,5,6,2,1,2,3,7,6,3 ...
- 三种Hash算法对比以及秒传原理.
三种Hash算法对比以及秒传原理 CRC (32/64) MD5 Sha1 分5个点来说 1.校验值长度 2.校验值类别 3.安全级别 4.应用场景 1).校验值长度 CRC(32/64) 分别 ...
- 机器学习---用python实现最小二乘线性回归算法并用随机梯度下降法求解 (Machine Learning Least Squares Linear Regression Application SGD)
在<机器学习---线性回归(Machine Learning Linear Regression)>一文中,我们主要介绍了最小二乘线性回归算法以及简单地介绍了梯度下降法.现在,让我们来实践 ...
- 创建B树,动态添加节点,并使用三种遍历算法对树进行遍历
ks17:algorithm apple$ cat btree_test.c ///********************************************************** ...
- Spark MLlib回归算法------线性回归、逻辑回归、SVM和ALS
Spark MLlib回归算法------线性回归.逻辑回归.SVM和ALS 1.线性回归: (1)模型的建立: 回归正则化方法(Lasso,Ridge和ElasticNet)在高维和数据集变量之间多 ...
随机推荐
- golang --写test测试用例
安装gotests插件自动生成测试代码: go get -u -v github.com/cweill/gotests/... 如何编写测试用例 由于go test命令只能在一个相应的目录下执行所有文 ...
- 【1】volatile关键字解析
volatile这个关键字可能很多朋友都听说过,或许也都用过.在Java 5之前,它是一个备受争议的关键字,因为在程序中使用它往往会导致出人意料的结果.在Java 5之后,volatile关键字才得以 ...
- Spring-Cloud之Hystrix熔断器-5
一.在分布式系统中,服务与服务之间的依赖错综复杂,一种不可避免的情况就是某些服务会出现故障,导致依赖于它们的其他服务出现远程调度的线程阻塞 Hystrix是Netflix 公司开源的一个项目,它提供了 ...
- java之mybatis之字段映射及多对一
1. 数据库中表的列名和实体类的属性名称不一致. 可以使用 resultMap来解决. <select id="findAll" resultMap="UserMa ...
- 强大的Grafana k8s 插件
原文参考: https://i4t.com/4152.html 参考:https://blog.csdn.net/mailjoin/article/details/81389700 插件链接:http ...
- mysql-数据备份与存储过程
目录 修改隔离级别 存储过程 什么是存储过程 用来干什么 三种数据处理方式 备份与恢复 修改隔离级别 修改全局的 set global transaction isolation level read ...
- 实战AudioToolbox--在iOS平台上播放音频
上午看了关于AudioToolbox.framework相关的资料,结合网上的资料对AudioToolbox的基本使用有了整体上的认识,上一篇文章 笔谈AudioToolbox(一) 中提到使用Aud ...
- day 08作业 预科
有如下值集合 [11,22,33,44,55,66,77,88,99,90...],将所有大于 66 的值保存至字典的第一个key中,将小于 66 的值保存至第二个key的值中 lt=[11,22,3 ...
- 转:ajax的AntiForgery和Authorize 以及ajax登录例子
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明.本文链接:https://blog.csdn.net/ashcn2001/article/det ...
- 申请软件著作权,wps显示代码行号功能
申请软件著作权时,要提交代码. 格式要求,每页不少于50行,怎么设置格式,保障每页至少50行呢? 选择[页面布局]---[行号]--[每页重编行号]即可显示出来,根据显示出来的行号,调整行距等格式即可 ...