android 入门开发
本示例讲解的是基本点有
1、使用SQLite数据库
2、对数据的新增,查询。
3、利用ViewActivity进行数据的呈现
代码是参考了网上各种代码,刚开始写,肯定有一些地方是有问题,我对JAVA代码也不熟悉,只是跟着网上学一学。
先来个项目全局图
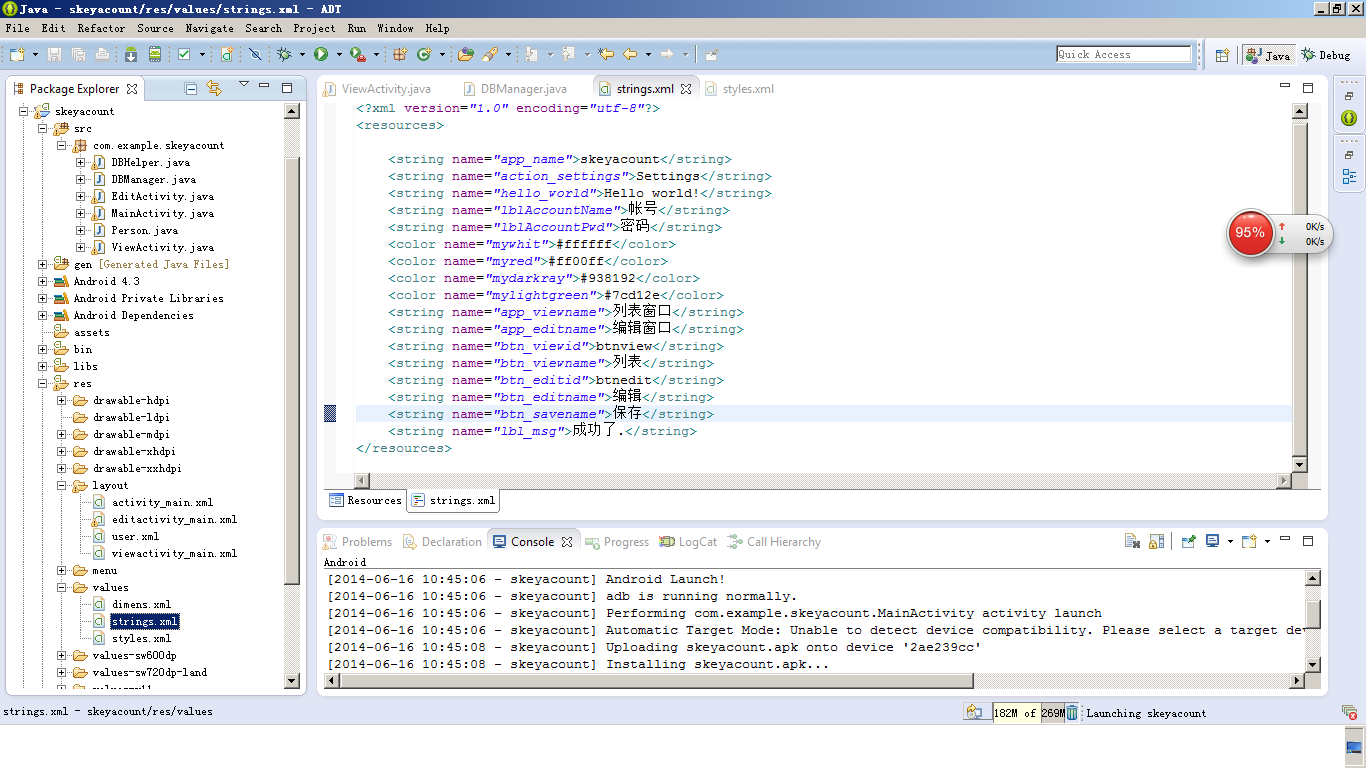
我是将代码部分进行了一下简单的分类
activity_main.xml是主界面,只有两个按钮
editactivity_main.xml是编辑界面,有两个畋
user.xml是呈现界面的设置,使用ListView中配置使用了该XML
viewactivity_main.xml是呈现的主界面
android 入门开发的更多相关文章
- 移动开发 android 入门开发 阶段视频
一直想把 android 的开发学习录制成视频,这里录制了一部分供大家学习. http://www.chuanke.com/s5402069.html 到这里,文档,源码,视频基本就全了,祝愿大家能够 ...
- Android入门开发时注意的两个问题
android开发中的问题: . 开发应用时要访问网络往往会忘记添加网络权限 <uses-permission android:name="android.permission.INT ...
- Android入门开发之销毁activity
使用: 销毁.关闭页面activity 如果打开下个页面的同时销毁了本页面,在下个页面无法返回本页面,每次打开APP应用就会先显示一张APP的介绍图.或者LOGO页面,延时几秒进入应用,进入后无法再返 ...
- [书目20160624]Android应用开发从入门到精通
卢海东 著 第1章 揭开神秘面纱——Android系统简介 1 1.1 认识Android系统 2 1.1.1 Android成长历程 2 1.1.2 发行版本 3 1.1.3 得到大 ...
- 一看就懂的Android APP开发入门教程
一看就懂的Android APP开发入门教程 作者: 字体:[增加 减小] 类型:转载 这篇文章主要介绍了Android APP开发入门教程,从SDK下载.开发环境搭建.代码编写.APP打包等步骤 ...
- Android Wear 开发入门
大家好,我是陆嘉杰,我是一名Android开发者.我想和大家进行一些技术交流,希望越来越多的人能和我成为好朋友. 大家都知道,智能手表是下一个开发的风口,而这方面的技术又属于前沿,所以和大家分享下An ...
- 我的新书《Android App开发从入门到精通》终于出版啦
前言 经过了两年多终于完成了这本书,2016年9月份开始写的,到今天为止2年零2个月,本书的内容大部分是去年完成的,看过我去年总结的读者可能知道,去年事情很多太忙了,导致本命年这本书没有上架(有点小小 ...
- Android GIS开发系列-- 入门季(14)FeatureLayer之范围查询
Android GIS开发系列-- 入门季(5),这篇文章中,我们知道如何去查找要素.现在有一个需求,查找某点5000米范围的要素,那如何来做呢?首先我们需要在地图上画个5000米半径的圆,然后根据Q ...
- Android WebRTC开发入门
在学习 WebRTC 的过程中,学习的一个基本步骤是先通过 JS 学习 WebRTC的整体流程,在熟悉了整体流程之后,再学习其它端如何使用 WebRTC 进行互联互通. 申请权限 Camera 权限 ...
随机推荐
- 关于使用Hadoop MR的Eclipse插件开发时遇到Permission denied问题的解决办法【转】
搭建了一个Hadoop的环境,Hadoop集群环境部署在几个Linux服务器上,现在想使用windows上的Java客户端来操作集群中的HDFS文件,但是在客户端运行时出现了如下的认证错误,被折磨了几 ...
- linux时间校对
在虚拟机中查看安装的linux时间,总是不对,于是查阅资料,有很多解决办法,我个人比较倾向于用ntpdate的方式更新时间. 感觉比较好用的一个方法: 输入date查看时间,发现不对,相差甚远!(当前 ...
- Transformer —— attention is all you need
https://www.cnblogs.com/rucwxb/p/10277217.html Transformer -- attention is all you need Transformer模 ...
- 学习10:Python重要知识
Python易忽略知识 (1)print 默认输出是换行的,如果要实现不换行需要在变量末尾加上 end="": (2)isinstance 和 type 的区别在于:type()不 ...
- JS高阶---闭包(循环遍历+监听)
大纲: 主体: (1)场景1:点击按钮显示点击的第几个 注意:伪数组每次循环时都会重新计算一次长度,所以最好提出去或者直接加到for循环内部 结果: 分析: 1.i为全局变量 解决方案: 1.下标法 ...
- 201871010104-陈园园 《面向对象程序设计(java)》第六——七周学习总结
201871010104-陈园园 <面向对象程序设计(java)>第六——七周学习总结 项目 内容 这个作业属于哪个课程 https://www.cnblogs.com/nwnu-daiz ...
- 201871010108-高文利《面向对象程序设计(java)》第十周学习总结
项目 内容 这个作业属于哪个课程 <任课教师博客主页链接> https://www.cnblogs.com/nwnu-daizh/ 这个作业的要求在哪里 <作业链接地址> ht ...
- robotframework-post request请求携带上一个请求返回的cookie
公司的接口服务需要先登录,获取服务端的cookie后,在后续的请求中携带这个cookie才能够访问 在尝试用RF工具进行自动化接口测试时,发现先访问登录接口之后,接着请求其他接口时没有自动携带上次请求 ...
- Nginx的代理配置(六)
一.正向代理 1. 指令说明 (1) resolver 这个用于设置DNS服务器的ip .DNS服务器的主要工作是进行域名解析,将域名映射为对应IP地址. 语法:resolver address .. ...
- SGD的动量(Momentum)算法
引入动量(Momentum)方法一方面是为了解决“峡谷”和“鞍点”问题:一方面也可以用于SGD 加速,特别是针对高曲率.小幅但是方向一致的梯度. 如果把原始的 SGD 想象成一个纸团在重力作用向下滚动 ...
