题解报告：hdu 1392 Surround the Trees（凸包入门）

Problem Description

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him? 
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.
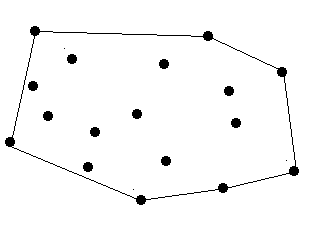There are no more than 100 trees.

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.
Zero at line for number of trees terminates the input for your program.

Output

The minimal length of the rope. The precision should be 10^-2.

Sample Input

9

12 7

24 9

30 5

41 9

80 7

50 87

22 9

45 1

50 7

0

Sample Output

243.06

解题思路：入门凸包！有一篇博文讲得非常好非常易懂，链接：凸包详解。再贴一张如何用叉积来判断栈顶的点是否为凸包上合法顶点的依据图。时间复杂度主要花在排序上为O(nlogn)。

以下是Graham扫描算法的演示--->逐步构建凸包的过程：

AC代码(62ms)：详细注释看代码。选取基点的标准是找到y值最小的点，如果有多个，选择最左边即横坐标最小的那个。

 #include<iostream>
 #include<string.h>
 #include<algorithm>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 const int maxn=;
 const double PI=acos(-1.0);
 struct node{int x,y;};
 node vex[maxn];//存入所有坐标点
 node stackk[maxn];//凸包中所有的点
 bool cmp1(node a,node b){//按点的坐标排序
     if(a.y==b.y)return a.x<b.x;//如果纵坐标相同，则按横坐标升序排
     else return a.y<b.y;//否则按纵坐标升序排
 }
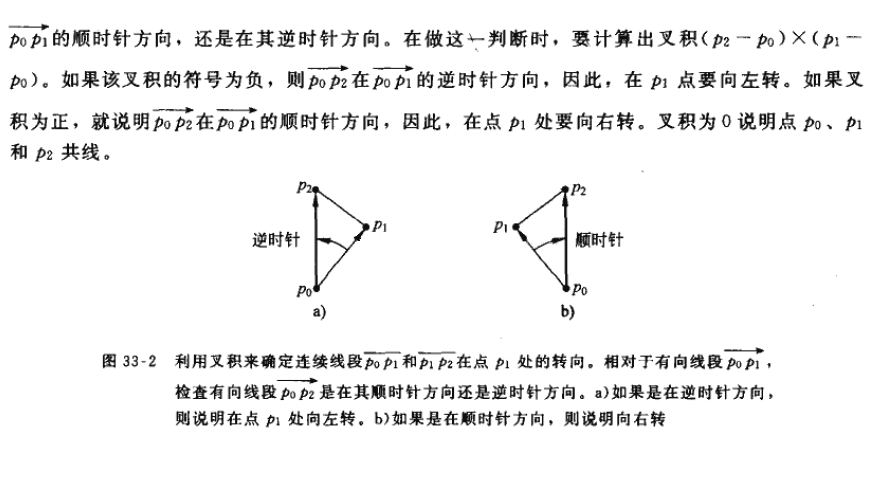
 bool cmp2(node a,node b){//以基点为坐标原点，极角按升序排，这里可用atan2函数或者叉积来进行极角排序，但是用atan2函数来排序效率高时间快，不过精度比叉积低
     double A=atan2(a.y-stackk[].y,a.x-stackk[].x);//返回的是原点至点(x,y)的方位角，即与x轴的夹角
     double B=atan2(b.y-stackk[].y,b.x-stackk[].x);
     if(A!=B)return A<B;//逆时针方向为正值，极角小的排在前面
     else return a.x<b.x;//如果极角相同，则横坐标在前面的靠前排列
 }
 int cross(node p0,node p1,node p2){//计算两个向量a、b（a=(x1,y1),b=(x2,y2)）的叉积公式：a×b=x1y2-x2y1 ===> p0p1=(x1-x0,y1-y0),p0p2=(x2-x0,y2-y0)
     return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
 }
 double dis(node a,node b){//计算两点之间的距离
     return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y));
 }
 int main(){
     int t;
     while(~scanf("%d",&t)&&t){
         for(int i=;i<t;++i)//输入t个点
             scanf("%d%d",&vex[i].x,&vex[i].y);
         if(t==)printf("%.2f\n",0.00);//如果只有一个点，则周长为0.00
         else if(t==)printf("%.2f\n",dis(vex[],vex[]));//如果只有两个点，则周长为两个点的距离
         else{
             memset(stackk,,sizeof(stackk));//清0
             sort(vex,vex+t,cmp1);//先按坐标点的位置进行排序
             stackk[]=vex[];//取出基点
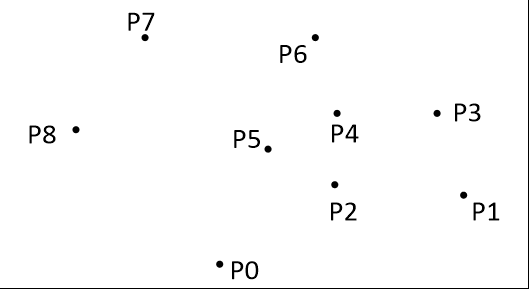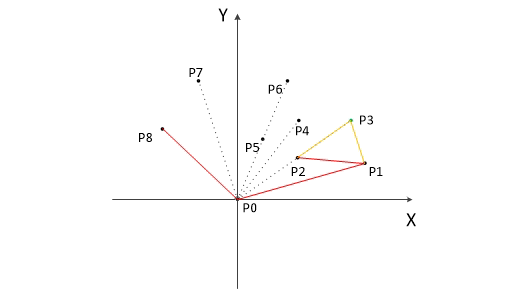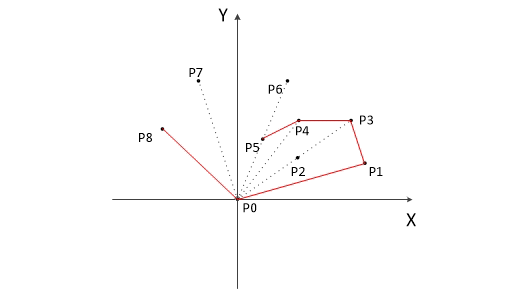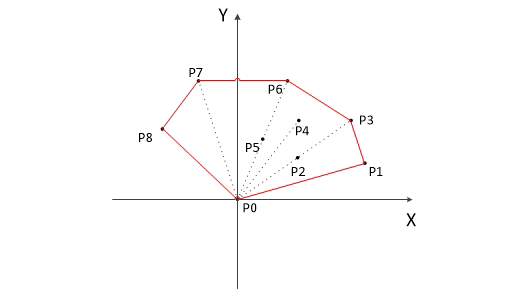
             sort(vex+,vex+t,cmp2);//将剩下的坐标点按极角进行排序，以基点为坐标原点
             stackk[]=vex[];//将凸包中的第二个点存入凸集中
             int top=;//当前凸包中拥有点的个数为top+1
             for(int i=;i<t;++i){//不断地找外围的坐标点
                 while(top>&&cross(stackk[top-],stackk[top],vex[i])<=)top--;//如果叉积为负数或0（0表示两向量共线），则弹出栈顶元素
                 //虽然第2个凸点显然是最外围的一点，但加上top>0保证了栈中至少有2个凸点
                 stackk[++top]=vex[i];
             }
             double s=;
             for(int i=;i<=top;++i)//计算凸包的周长
                 s+=dis(stackk[i-],stackk[i]);
             s+=dis(stackk[top],vex[]);//最后一个点和第一个点之间的距离
             printf("%.2f\n",s);
         }
     }
     return ;
 }

AC代码二(31ms)：Andrew算法，一次坐标排序，两次构造成一个完整的凸包，时间复杂度为O(nlogn)，但实际上比Graham扫描算法快很多，具体讲解-->凸包解法总结。

 #include<iostream>
 #include<string.h>
 #include<algorithm>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 const int maxn=;
 const double PI=acos(-1.0);
 struct node{int x,y;}vex[maxn],stackk[maxn];
 bool cmp(node a,node b){//按点的坐标排序
     return (a.y<b.y)||(a.y==b.y&&a.x<b.x);
 }
 int cross(node p0,node p1,node p2){
     return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
 }
 double dis(node a,node b){
     return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y));
 }
 int main(){
     int t;
     while(~scanf("%d",&t)&&t){
         for(int i=;i<t;++i)//输入t个点
             scanf("%d%d",&vex[i].x,&vex[i].y);
         if(t==)printf("%.2f\n",0.00);
         else if(t==)printf("%.2f\n",dis(vex[],vex[]));
         else{
             memset(stackk,,sizeof(stackk));//清0
             sort(vex,vex+t,cmp);//一次坐标排序，两次构造成一个完整的凸包
             int top=-;
             for(int i=;i<t;++i){//构造凸包下侧
                 while(top>&&cross(stackk[top-],stackk[top],vex[i])<=)top--;
                 stackk[++top]=vex[i];
             }
             for(int i=t-,k=top;i>=;--i){//构造凸包上侧，默认此时凸包中只有一个顶点n-1，因此top要大于k，起点再被包含一次且一定被包含
                 while(top>k&&cross(stackk[top-],stackk[top],vex[i])<=)top--;
                 stackk[++top]=vex[i];
             }
             double s=;
             for(int i=;i<=top;++i)//计算凸包周长
                 s+=dis(stackk[i-],stackk[i]);
             printf("%.2f\n",s);
         }
     }
     return ;
 }