数值优化（Numerical Optimization）学习系列-无梯度优化（Derivative-Free Optimization）

数值优化（Numerical Optimization）学习系列-无梯度优化（Derivative-Free Optimization）

2015年12月27日 18:51:19 下一步 阅读数 4357更多

分类专栏： 数值优化

 

版权声明：本文为博主原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/fangqingan_java/article/details/48946903

概述

在实际应用中，有些目标函数的梯度不容易计算，即使使用有限差分等近似算法，也会因为噪声的存在导致结果不精确。无梯度优化算法（DFO-Derivative-Free Optimization）可以在不计算梯度的情况下进行问题的最优化，主要有两类思路，一是根据目标函数的样本进行拟合，对拟合函数进行最优化；二是用一些启发式算法。 
1. 有限差分和误差 
2. 基于模型近似的方法 
3. 坐标和模式搜索方法 
4. 其他DFO方法 
5. 总结

有限差分和误差

有限差分方法在某些情况下可能会有一定的误差，例如如果函数值需要通过随机试验进行模拟，此时会引入人为误差或者仪器误差。 
因此对问题进行建模时，将误差引入目标函数中，然后利用有限差分和梯度相关算法进行优化。

 

f(x)=h(x)+ϕ(x)f(x)=h(x)+ϕ(x)

其中函数h表示某平滑函数，ϕϕ表示误差分布函数，该函数可以和参数x有关也可以无关。

对误差进行建模后，然后利用中心有限差分方法，进行梯度的计算

 

∂f∂xi≈f(x+ϵei)−f(x−ϵei)2ϵ∂f∂xi≈f(x+ϵei)−f(x−ϵei)2ϵ

噪声水平（Noise Level）定义为： 
在x附近噪声最大值。η(x;ϕ)=sup||z−x||≤ϵ|ϕ(z)|η(x;ϕ)=sup||z−x||≤ϵ|ϕ(z)|

此时使用有限差分方法，近似误差来源于固有误差和噪声误差。

基于模型的方法

主要思路是，在第k步迭代时，基于该点进行模型近似，通过采样推导出模型中的参数，基于该模型进行最优化计算。

二次模型近似

在第k步迭代时，构建一个二次模型进行近似

 

mk(xk+p)=c+gTp+12pTGpmk(xk+p)=c+gTp+12pTGp

，其中g和G分别表示函数f的一阶和二阶梯度。 
由于该模型参数c、g和G都是未知的，因此需要1+n+(n+1)n/2=(n+1)(n+2)/2个未知数需要计算。 
所以基于点Xk需要采样这么多个点进行未知数计算。 
样本Y=y1,y2...yqY=y1,y2...yq，假设该集合中的点值都比x_k大。根据拟合等式mk(yl)=f(yl)mk(yl)=f(yl) 
此时可以唯一确定模型m，然后利用信赖域或者梯度方法进行最优化。

在实际应用中，我们仅需要更新模型M即可，不用每次都重新计算。可以选择合适方便计算的基函数。

算法过程如下 
 

算法过程如下 
1. 构建插值集合Y=y1,y2...yqY=y1,y2...yq需要保证线性方式的解存在。 
2. 求解插值方程 
3. 根据二次模型进行最优解计算 
4. 根据最优解的效果，决定是否采用该解。 
5. 根据一个几何过程更新几何Y。

二次模型的缺点：样本点选择是O(n^2)的，如果维度越高计算复杂度越大。因此可以考虑线性模型，此时只有O(n+1)个样本需要求解，复杂度会降低。

坐标和模式搜索方法

不同于梯度相关的算法，基于模式搜索方法的搜索方向都是事先确定好的，该方法需要从方向集合中选择一个下降方向作为搜索方向并且更新该方向集合，之后利用线搜索决定步长，逐步迭代得到最优解。 
坐标下降是模式搜索方法中的一个特例。

坐标搜索方法（Coordinate SearchMethod）

该方法也称之为坐标下降法或者变量交替方法，主要思路是依次沿着坐标轴方向进行线搜索。 
详细过程如下 
1. 选择某个迭代点x=(x1,x2…xn)，固定x2…xn，优化x1使得目标函数最小 
2. i=2..n 优化x_i使得目标函数最小 
3. 重复以上步骤 
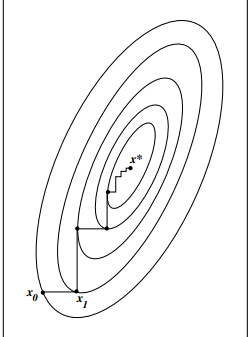
对于二维情况下，搜索过程如下 

1. 从上图中可以看出，对于条件数比较大的问题，收敛速度非常低。
2. 实际中，如果沿着线性独立的搜索方向搜索，可能不能保证收敛。但是优点是不需要计算梯度，并且对于变量松耦合的情况下，收敛速度可以接受。
3. 另外为了进行优化，搜索方向可以选择为{e1,e2...en,en−1...e1e1,e2...en,en−1...e1}

模式搜索方法

每次搜索方向都是从一个“结构集”中选取，找到某个下降点，进行线搜索，否则修改步长，重复该过程。 
该方法会受到噪声点、函数值不精确、不平滑的影响。算法过程如下 
算法描述如下 
定义 
* DkDk表示第k迭代的方向集合 
* γkγk表示第k步线性搜索参数，即步长，如果找到下降方向，则xk+γkpkxk+γkpk为最优点 
* ρ(t)ρ(t)为递增函数，并且当t接近0时，该函数值为0 
算法过程 
1. 初始化搜索方向集合D0D0 
2. 循环迭代一下过程，直到搜索步长满足给定阈值。 
3. 如果找到满足一定下降条件的搜索方向，则修改最优值点，并且增大步长。 
4. 否则减少步长 
关键点

1. 初始化搜索方向集合D0D0如何选取，需要保证包含最优解的方向。
2. 有理论保证如果搜索方向满足一下条件，则一定能保证收敛。
    
   κ(Dk)=minv∈Rnmaxp∈DkvTp||v||||p||≥δκ(Dk)=minv∈Rnmaxp∈DkvTp||v||||p||≥δ
    
   βmin≤||p||≤βmaxp∈Dkβmin≤||p||≤βmaxp∈Dk
3. 条件1说明需要保证最少有一个搜索方向和最优方向的夹角小于90，即cos(θθ) > δδ，不能再相反的方向，否则不容易收敛。
4. 条件2说明搜索方向的模不能相差太大，因此搜索步长统一进行缩放。
5. 满足条件的搜索方向有 {e1,e2...en,−e1...−ene1,e2...en,−e1...−en},供2n个搜索方向或者{pi=12ne−ei,pn+1=12nepi=12ne−ei,pn+1=12ne}，供n+1个点
6. 递增函数可以选择为ρ(t)=Mt3/2ρ(t)=Mt3/2

其他DFO算法

共轭方向算法

类似于共轭梯度方法，该方法的目标是最优化

 

f(x)=12xTAx−bTxf(x)=12xTAx−bTx

，不同点在于共轭方向的计算仅仅依靠函数值得到，不依赖梯度的计算。

Parallel subspace property

通过该方法可以找到一系列共轭方向，并且沿着该方向可以得到最优解，以二维情况为例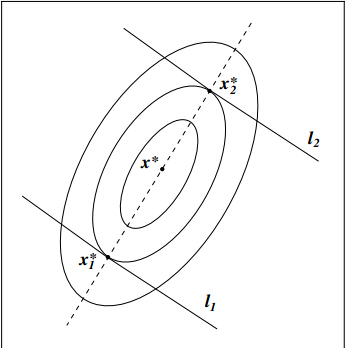 
 
如上图如果直线l1和l2平行，并且x1*和x2*是目标函数沿着该直线的最优解，则x1*-x2*共轭于直线的法向量。 
因此只要沿着某两个平行子空间寻找最优解，则最优解的差就共轭于该平面的法向量。 
假设{p1,p2...plp1,p2...pl}是线性独立的向量，定义两个平行平面

 

s1={x1+∑i=1..lαipi}s1={x1+∑i=1..lαipi}

 

s2={x2+∑i=1..lαipi}s2={x2+∑i=1..lαipi}

并且目标函数沿着该平面的最优解分布为x1*和x2*，则x2*-x1*共轭于p1,p2...plp1,p2...pl

证明很简单 
由于x1*是最优解，则有

 

∂f(x∗1+αipi)∂αi=∂f(x∗1+αipi)pi∂f(x1∗+αipi)∂αi=∂f(x1∗+αipi)pi

，当αi=0，∇f(x∗1)pi=0，根据最优化条件得到αi=0，∇f(x1∗)pi=0，根据最优化条件得到

 

0=(∇f(x∗1)−∇f(x∗2))pi=(Ax1−b−Ax2+b)pi=(x1−x2)Api0=(∇f(x1∗)−∇f(x2∗))pi=(Ax1−b−Ax2+b)pi=(x1−x2)Api

根据共轭条件可以得到。

Nelder-Mead 方法

也叫做Nelder-Mead simplex reflection方法。 
保存n+1个点，并且这些点构成一个单纯性，在每次循环中搜索使得函数值最低的点，去掉后，用其他更好的点替代。

Implicit Filtering方法

对比于带有噪声的有限微分方法，适用于noise level随着迭代减小的情形。

总结

通过该小结的学习，可以了解到 
1. 对于梯度不可求的复杂函数，可以通过DFO的方式进行优化 
2. 通过随机试验估计函数值的最优化问题，可以考虑带噪声的有限差分。 
3. 了解基于模型的方法，但是复杂度可能会比较大 
4. 了解坐标下降法和模式搜索算法 
5. 了解基于共轭方向等其他方法。

数值优化（Numerical Optimization）学习系列-惩罚和增广拉格朗日方法（Augmented Lagrangian Methods）

阅读数 1431

概述求解带约束的最优化问题，一类很重要的方法就是将约束添加到目标函数中，从而转换为一系列子问题进行求解，最终逼近最优解。关键问题是如何将约束进行转换。本节主要介绍1.二次惩罚方...博文来自： kkwant的博客

 

qpOASES：使用说明（翻译）

阅读数 1431

qpOASES使用说明1 说明2 主要步骤创建QProblem类的实例第一个QP的初始化和求解求解后续QP一个实列设置自己的实例本文将在几分钟内向您解释如何通过qpOASES解决二次规划（QP）问题或...博文来自： 博客

数值优化（Numerical Optimization）学习系列-目录

阅读数 1万+

概述数值优化对于最优化问题提供了一种迭代算法思路，通过迭代逐渐接近最优解，分别对无约束最优化问题和带约束最优化问题进行求解。该系列教程可以参考的资料有1.《NumericalOptimization2...博文来自： fangqingan_java的专栏

Derivative-Free and Blackbox Optimization

11-24

这是关于黑盒优化的电子书，高清，最新版本，经典著作，英文版

下载

qpOASES库keil移植的问题

02-26

-问答

qpOASES: a parametric active-set algorithm for quadratic programming

11-12

qpOASES: a parametric active-set algorithm for quadratic programming，一种QP问题求解方法，Apollo中的MPC控制使用该方法用于

下载

如何解决labview循环结构中调用matlab节点后，程序运行缓慢的问题

02-28

-问答

神经网络控制学习笔记——神经网络背景1

阅读数 686

神经网络控制学习笔记——BackgroundonNeuralNetworks1因为不太熟悉怎么用CSDN的编辑器来编辑文本，也懒得花时间学了。这里贴上在word写好后转成pdf的截图好了。相关的引用文...博文来自： huangdianye

数值优化（Numerical Optimization）学习系列-概述

阅读数 1万+

数值优化的学习过程是长期的、是枯燥的也是最有用的，一旦入门对机器学习者、算法工作者都会有很大的帮助。在此记录NumericalOptimization的学习、思考和实践。...博文来自： fangqingan_java的专栏

网上兼职不靠谱，赚不到钱？来这教你轻松挣几百！大观

数值优化（Numerical Optimization）学习系列-大规模无约束最优化（Large-Scale Unconstrained Optimization）

阅读数 2128

概述当最优化问题参数个数增加，求解问题所需要的时间和空间复杂度会增加。计算时间和空间是一个权衡，只需要存储一阶梯度时，时间复杂度可能为超线性；如果利用Hessian矩阵可以达到二次收敛，但是需要o(n...博文来自： fangqingan_java的专栏

qpOASES：特殊QP类型的求解1（翻译）

阅读数 552

ad博文来自： 博客

关注

kkwant

498篇文章

排名:9000+

关注

weixin_40709533

9篇文章

排名:千里之外

关注

Seehidre

637篇文章

排名:7000+

几种常见梯度优化方法

阅读数 2159

优化算法是机器学习领域的重要内容，本文介绍几种常见的无约束的优化算法，并给出Python实例。关于无约束问题优化方法的一般讨论请参考此文。梯度下降法动量法共轭梯度法自然梯度法梯度下降法动量法共轭梯度法...博文来自： 止于至玄

导数的理解

阅读数 2471

导数是用来找到“线性近似”的数学工具在我学习微积分的过程中，我对导数的认知经历了三次变化：导数是变化率、是切线的斜率、是速度、是加速度导数是用来找到“线性近似”的数学工具导数是线性变换我们认为，导数是...博文来自： xdy1120的博客

Apollo代码学习(六)—模型预测控制(MPC)

阅读数 1万+

Apollo代码学习—模型预测控制前言模型预测控制预测模型滚动优化反馈矫正前言查看Apollo中关于MPC_controller的代码可以发现，它的主体集成了横纵向控制，在计算控制命令时，计算了横纵向...博文来自： follow轻尘的博客

Matlab 不等式 线性方程式最优解

08-02

-问答

MPC求解（基于apollo代码的理解）

阅读数 441

MPC求解（基于apollo代码的理解）参考follow轻尘并做了修正方向盘控制模型[RajamaniR.VehicleDynamicsandControl[M].SpringerScience,20...博文来自： weixin_41399470的博客

百度Apollo自动驾驶专题讲座笔记之运动规划模块

阅读数 145

主讲人：范昊阳包括运动规划基础概述、自动驾驶运动规划、环境下运动规划、运动规划内优化、Apolloemplanner开发环节、强化学习与数据驱动方法七个部分第一部分：运动规划基础概述1、什么是规划问题...博文来自： zhongweidu3的博客

如何在服务器中保存OpenAI gym库中的视频

03-05

-问答

qpOASES使用笔记

阅读数 261

概述qpOASES是一个开源c++项目，是一个可结构开发的有效集求解器（structure-exploitingactive-setQPsolver）。qp可用于解决具有一下标准形式的问题：H为半正定...博文来自： qq_41986495的博客

python，matlab,C++ 凸优化库——anaconda spyder->cvxpy,matlab->cvx,C++->qpOASES

阅读数 356

python:使用spyder安装所需库，包时需要在控制台输入命令!pipinstallxxxx但是有可能源不太好，导致安装失败因此最好去官网下载，然后将下载包放置到工作空间，使用!pipinstal...博文来自： qinze5857的博客

QP问题的解法（拉格朗日乘子法）

阅读数 1万+

function[x,lam,fval]=qlag(H,A,b,c)%拉格朗日法求解二次规划问题%minf(x)=0.5*x'Hx+c'x,s.t.Ax=b%input:H,c分别是目标函数的矩阵和向...博文来自： 小明知道的专栏

Python——使用scipy求解带约束的最优化问题

阅读数 1013

我们要求解的最优化问题的形式如下：min f(x)s.t.gi(x)>0,i=1,...,mhj(x)=0,j=1,...,n\begin{aligned}min\f(x)\\...博文来自： HappyRocking的专栏

二次规划——学习笔记

阅读数 5890

什么是二次规划？https://wenku.baidu.com/view/dafc28a99f3143323968011ca300a6c30c22f1bd.html二次规划是最简单的约束非线性规划问题...博文来自： huangdianye

Eigen学习

阅读数 472

Eigen学习一些非矩阵类型，可以按照矩阵的形式运算#include<Eigen/Core>#include&amp...博文来自： 朝闻雨的博客

二次型求导

阅读数 1549

二次型求导博文来自： jinglingsheshou的博客

rqt_plot工具——ROS中查看变量时间趋势线

阅读数 1405

rqt_plot工具——ROS中查看变量时间趋势线工欲善其事，必先利其器本篇博文依旧是小白教程，最近在写利用二次规划方法优化机械臂关节轨迹的代码。想要通过查看误差变量的时间趋势线看一下控制效果。百度了...博文来自： huangdianye

roscpp添加第三方依赖库——以QuadProg++为例

阅读数 594

roscpp添加第三方依赖库——以QuadProg++为例roscpp添加第三方依赖库——以QuadProg++为例【小白教程，不喜勿喷】昨天倒腾了一晚上，在roscpp的C++代码中添加求解二次规划...博文来自： huangdianye

[最优化]不等式约束的优化问题求解

阅读数 4103

不等式约束的优化问题求解与前文讨论的只含等式约束的优化问题求解类似，含不等式约束的优化问题同样可以用拉格朗日乘子法进行求解对于一般形式的优化问题：minimizef(x)subject&nbs...博文来自： Math & Code

Installing qpOASES

阅读数 304

InstallingqpOASESqpOASESisself-contained!ExceptforacoupleofstandardClibraries,nofurtherexternalsoftw...博文来自： tap880507的博客

no kernel image is available for execution on the device，计算能力不匹配的问题？

03-05

-问答

openssl移植到armBN_mod_inverse:no inverse

03-14

-问答

画图问题，怎样用R语言将多个图片连接在一个圆形上？如下图

02-26

-问答

KUKA KR-16串联6轴机器人D-H坐标系建立以及参数确定问题

04-22

-问答

道路的修建，一个最优化的规划问题的算法，怎么用C语言的代码来实现呢

03-28

-问答

Opencv里vector<Mat>的问题

03-04

-问答

库文件更新，工程本地需要更新库重新编译吗？

03-15

-问答

基于【Apollo】进程异常崩溃定位方法

阅读数 807

现象在dreamview里面，打开Navi_planning或者Planning模块的开关，开关运行一段时间后会自动关闭并重新开启。定位过程查看dreamview代码，模块开关定义在modules/d...博文来自： sunyoop的博客

ubuntu 16.04下安裝和配置ros（ORB-SLAM-A）

阅读数 2339

書上和網上關於ubuntu下安裝ros的文章很多，但是很多介紹的不完整，並且ubuntu和ros之間其實是有版本對應關系的，並不是所有的ros都能安裝到所有的ubuntu上，（很多書上或者文章介紹用的...博文来自： 开源节流

【Apollo】模拟运行

阅读数 1322

资源：1.论坛：http://www.51apollo.com2.gitlab上的docs，查找方式：在vscode中搜索关键字3.gitlab上的Issues4....博文来自： sunyoop的博客

算法工程师大致是做什么的?大观

使用CVXPY遇到个问题，请教。。

12-06

我用的CVXPY做最优化，一组数据昨天还能跑出结果的，刚才再一跑就出现这个 Internal problem occured in ECOS while setting up the problem的论坛

数值优化（Numerical Optimization）学习系列-信赖域方法

阅读数 9833

信赖域方法和线搜索类似都是迭代方法，与其不同的是，每次迭代时，在一个选定的可信赖区域内，选择当前迭代点的近似模型mkm_k，然后计算最优步长；如果步长不合适，可以对区域进行缩放。该小结主要介绍：信赖域...博文来自： fangqingan_java的专栏

数值优化（Numerical Optimization）学习

阅读数 1972

数值优化学习参考CSDN博客博文来自： u012238433的博客

matlab学习optimization tools （solve中各方法的理解应用）

阅读数 827

1.quadprog二次规划的函数Matlab中二次规划的数学模型可表述如下其中H是把目标函数二次项部分进行实对称矩阵，？？？这个什么意思？f是线性函数的列向量。例求解二次规划得到h=[4,-4;-4...博文来自： ZC496496的博客

【优化算法】基于梯度的优化算法

阅读数 890

优化指的是改变xxx以最大化或最小化某个函数f(x)f(x)f(x)的任务.我们通常以最小化f(x)f(x)f(x)指代大多数的最优化问题，最大化可以通过最小化−f(x)−f(x)-f(x)来实现。我...博文来自： 鹅城视觉驿站

有关梯度优化方法学习总结

阅读数 504

背景在机器学习领域，待解决的问题往往抽象建模成代价函数（costfunction），求解代价函数的最优解便是我们解决这个问题的目标。代价函数的求解便是优化过程，我们需要找到该函数的极小值，最好是最小值...博文来自： Yang_tech

基于梯度的优化方法

阅读数 3985

1.优化指的是改变x以最小化或最大化的某个函数f(x)的任务我们通常以最小化f(x)指代大多数最优化问题。最大化可经由最小化算法-f(x)来实现。我们希望最小化或最大化的函数叫目标函数，当我们对其进行...博文来自： Hansry的博客

webpack4 optimization配置

阅读数 5978

从webpack4开始官方移除了commonchunk插件，改用了optimization属性进行更加灵活的配置，这也应该是从V3升级到V4的代码修改过程中最为复杂的一部分，下面的代码即是optimi...博文来自： 柏灿的博客

3.webpack的optimization配置

阅读数 867

阿达博文来自： weixin_43678786的博客

机器学习，最优化数值计算常用算法

阅读数 705

一机器学习表示及数值求解原理大部分机器学习，尤其是神经网络、深度网络，最优化一个经验损失函数（通常带有正则项），损失函数在某个样本点可表示为：L(β⃗&amp;amp;amp;amp;amp;amp;...博文来自： 数学民工

数值最优化方法

阅读数 2167

算法来源：《数值最优化方法~高立》算法目的：实现函数的局部最优化寻找，以二元函数为例，展示了最速下降法和牛顿寻优的算法过程主要Python模块：numpy,sympy（1）Python实现（2）MAT...博文来自： Dreamer_Tina的博客

c# linq原理 c# 装箱有什么用 c#集合 复制 c# 一个字符串分组 c++和c#哪个就业率高 c# 批量动态创建控件 c# 模块和程序集的区别 c# gmap 截图 c# 验证码图片生成类 c# 再次尝试 连接失败

没有更多推荐了，返回首页