普利姆算法(prim)
普利姆算法(prim)求最小生成树(MST)过程详解
 1
1 2
2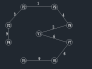 3
3 4
4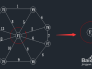 5
5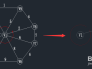 6
6 7
7
分步阅读
生活中最小生成树的应用十分广泛,比如:要连通n个城市需要n-1条边线路,那么怎么样建设才能使工程造价最小呢?可以把线路的造价看成权值求这几个城市的连通图的最小生成树。求最小造价的过程也就转化成求最小生成树的过程,则最小生成树表示使其造价最小的生成树。
那么怎么样用普利姆算法(prim算法)求最小生成树(MST)?
此以图例方式详述prim算法求最小生成树过程,希望对大家有帮助!
工具/原料
- 普利姆算法(prim算法)
- 最小生成树
一、最小生成树相关基础知识
- 1
最小生成树相关概念:
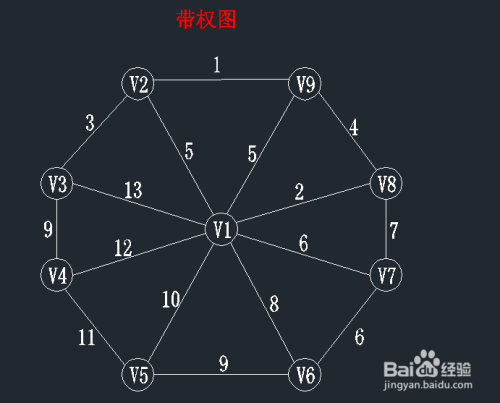
带权图:边赋以权值的图称为网或带权图,带权图的生成树也是带权的,生成树T各边的权值总和称为该树的权。
最小生成树(MST):权值最小的生成树。
生成树和最小生成树的应用:要连通n个城市需要n-1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。
- 2
最小生成树的性质:
MST性质:假设G=(V,E)是一个连通网,U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必存在一棵包含边(u,v)的最小生成树。
构造网的最小生成树必须解决下面两个问题:
(1)尽可能选取权值小的边,但不能构成回路;
(2)选取n-1条恰当的边以连通n个顶点;
 END
END
二、普利姆算法(prim算法)基本思想
- 1
prim算法基本思想:
假设G=(V,E)是连通的,TE是G上最小生成树中边的集合。算法从U={u0}(u0∈V)、TE={}开始。重复执行下列操作:
在所有u∈U,v∈V-U的边(u,v)∈E中找一条权值最小的边(u0,v0)并入集合TE中,同时v0并入U,直到V=U为止。
此时,TE中必有n-1条边,T=(V,TE)为G的最小生成树。
Prim算法的核心:始终保持TE中的边集构成一棵生成树。
看了上面一大段文字是否感觉有点晕?为了便于大家更好的理解,接下来进行算法过程的分步图解!
 END
END
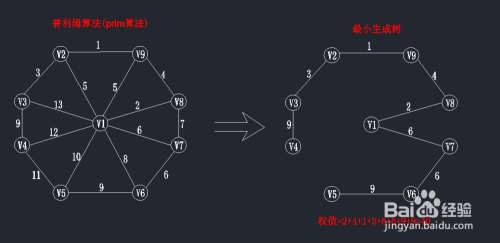
三、普利姆求最小生成树算法过程图解
- 1
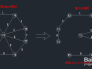
第一步:随意选取起点
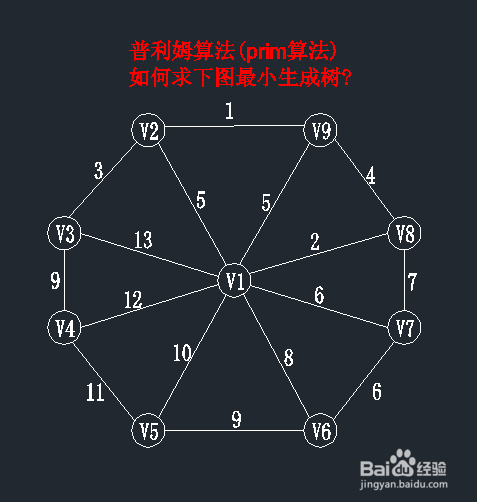
图中有9个顶点v1-v9,集合表示为:V={v1,....,V9},每条边的边权值都在图上;在进行prim算法时,我们先随意选择一个顶点作为起始点(起始点的选取不会影响最小生成树结果),在此我们一般选择v1作为起始点,现在我们设U集合为当前所找到最小生成树里面的顶点,TE集合为所找到的边。
状态如下:U={v1}; TE={};
- 2
第二步:在前一步的基础上寻找最小权值
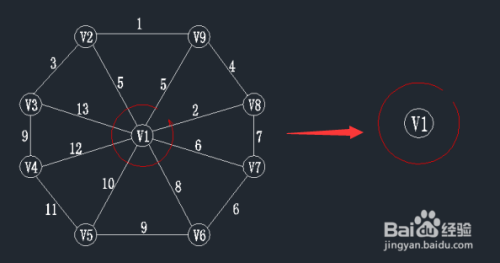
查找一个顶点在U={v1}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v1-v8的权值最小为2,那么将v8加入到U集合,(v1,v8)加入到TE。
状态如下:U={v1,v8}; TE={(v1,v8)};
- 3
第三步:继续寻找最小权值
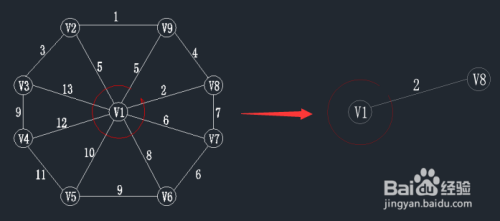
查找一个顶点在U={v1,v8}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v8-v9的权值最小为4,那么将v9加入到U集合,(v8,v9)加入到TE。
状态如下:U={v1,v8,v9}; TE={(v1,v8),(v8,v9)};
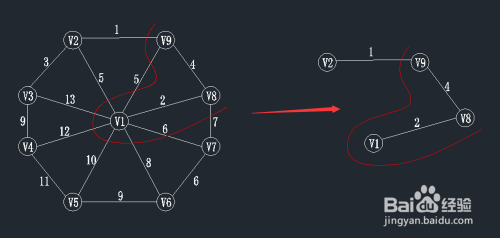
- 4
第四步:在前一步的基础上,继续寻找最小权值
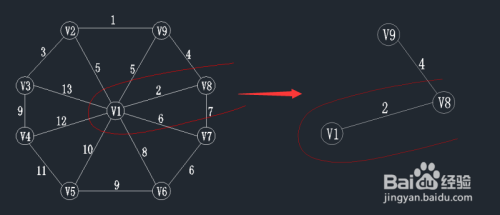
查找一个顶点在U={v1,v8,v9}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v9-v2的权值最小为1,那么将v2加入到U集合,(v9,v2)加入到TE。
状态如下:U={v1,v8,v9,v2};
TE={(v1,v8),(v8,v9),(v9,v2)};
- 5
第五步:继续在前一步的基础上,寻找最小权值
查找一个顶点在U={v1,v8,v9,v2}集合中,另一个顶点在V-U集合中的最小权值,如下图,在红线相交的线上找最小值。
通过图中我们可以看到边v2-v3的权值最小为3,那么将v3加入到U集合,(v2,v3)加入到TE。
状态如下:U={v1,v8,v9,v2,v3};
TE={(v1,v8),(v8,v9),(v9,v2),(v2,v3)};
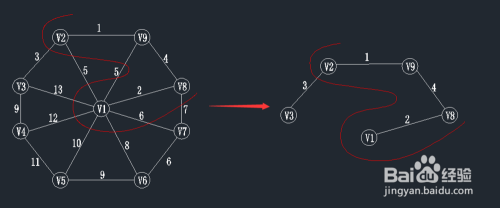
- 6
第五~九步:继续在前一步的基础上,寻找最小权值
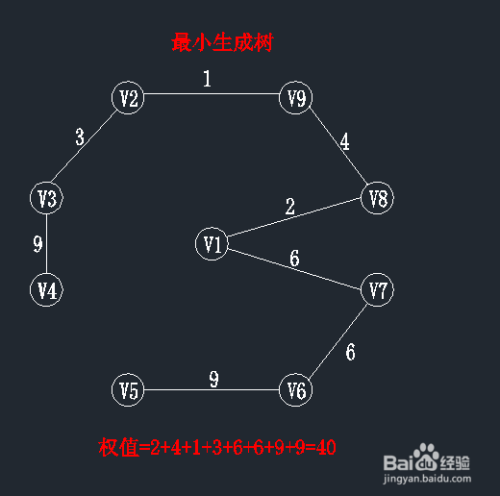
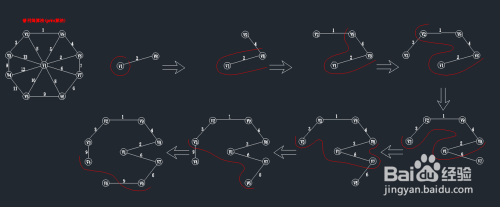
如此循环一下直到找到所有顶点为止。到这大家应该对普利姆算法求解最小生成树的过程有所知晓,但需注意以下三点:
(1)每次都选取权值最小的边,但不能构成回路,构成环路的边则舍弃。如图中的(v1,v9),(v1,v2)等构成回路舍弃
(2)遇到权值相等,又均不构成回路的边,随意选择哪一条,均不影响生成树结果。如图中的(v3,v4),(v6,v5)权值均为9,选择哪一条在先均不影响最小生成树的生成结果。
(3)选取n-1条恰当的边以连通n个顶点。
完整的算法步骤如图所示:
 END
END
四、小结
- 1
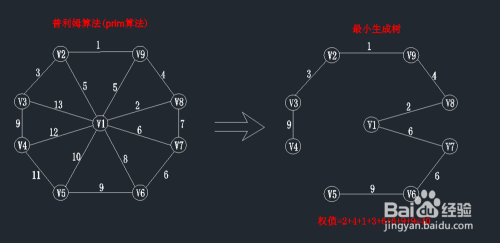
(1)最小生成树(MST)是指权值最小的生成树。
(2)prim算法是求最小生成树的算法之一,其他算法还有kruskal算法
(3)其时间复杂度为O(n^2),与边得数目无关。prim算法适合稠密图。
 END
END
注意事项
- (1)每次都选取权值最小的边,但不能构成回路,构成环路的边则舍弃。
- (2)遇到权值相等,又均不构成回路的边,随意选择哪一条,均不影响生成树结果
- (3)选取n-1条恰当的边以连通n个顶点
普利姆算法(prim)的更多相关文章
- c/c++ 用普利姆(prim)算法构造最小生成树
c/c++ 用普利姆(prim)算法构造最小生成树 最小生成树(Minimum Cost Spanning Tree)的概念: 假设要在n个城市之间建立公路,则连通n个城市只需要n-1条线路.这时 ...
- 最小生成树-普利姆算法eager实现
算法描述 在普利姆算法的lazy实现中,参考:普利姆算法的lazy实现 我们现在来考虑这样一个问题: 我们将所有的边都加入了优先队列,但事实上,我们真的需要所有的边吗? 我们再回到普利姆算法的lazy ...
- 最小生成树-普利姆算法lazy实现
算法描述 lazy普利姆算法的步骤: 1.从源点s出发,遍历它的邻接表s.Adj,将所有邻接的边(crossing edges)加入优先队列Q: 2.从Q出队最轻边,将此边加入MST. 3.考察此边的 ...
- 最小生成树练习3(普里姆算法Prim)
风萧萧兮易水寒,壮士要去敲代码.本女子开学后再敲了.. poj1258 Agri-Net(最小生成树)水题. #include<cstdio> #include<cstring> ...
- 最小生成树-普利姆(Prim)算法
最小生成树-普利姆(Prim)算法 最小生成树 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一种特殊的图),或者 ...
- 图论---最小生成树----普利姆(Prim)算法
普利姆(Prim)算法 1. 最小生成树(又名:最小权重生成树) 概念:将给出的所有点连接起来(即从一个点可到任意一个点),且连接路径之和最小的图叫最小生成树.最小生成树属于一种树形结构(树形结构是一 ...
- HDU 1879 继续畅通工程 (Prim(普里姆算法)+Kruskal(克鲁斯卡尔))
继续畅通工程 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Sub ...
- 算法与数据结构(五) 普利姆与克鲁斯卡尔的最小生成树(Swift版)
上篇博客我们聊了图的物理存储结构邻接矩阵和邻接链表,然后在此基础上给出了图的深度优先搜索和广度优先搜索.本篇博客就在上一篇博客的基础上进行延伸,也是关于图的.今天博客中主要介绍两种算法,都是关于最小生 ...
- POJ-2421-Constructing Roads(最小生成树 普利姆)
Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 26694 Accepted: 11720 Description The ...
随机推荐
- 分享几个好用的ui框架,以便开发
1:Layui--经典模块化前端框架 地址:https://www.layui.com/ 2:iview--基于 Vue.js 的高质量 UI 组件库 地址:http://v1.iviewui.com ...
- 多商铺平台手机电脑自适应宣传展示平台店铺javassh项目代码线上
部署运行:eclipse 建议使用jdk 1.8 + ,Tomcat 8.0 + 系统介绍: 1.网站后台采用主流的 SSH框架 jsp JSTL,网站前台采用Angular jS框架 2.网站前端采 ...
- 石子合并2(环形求最优解 区间dp)
题目描述 在一个圆形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分. 试设计出1个算法,计算出将N堆石子合并成1 ...
- Building(单调栈+凸包)
Problem Description Once upon a time Matt went to a small town. The town was so small and narrow tha ...
- Mysql慢查询(分析工具)
慢查询分析工具[mysqldumpslow] 常用的慢查询日志分析工具 汇总除查询条件外其他完全相同的SQL,并将分析结果按照参数中所指定的顺序输出 语法: mysqldumpslow -s r -t ...
- mac如何安装YaPi
首先介绍一下YaPi是干什么的. 帮助开发者轻松创建.发布.维护 API,YApi 还为用户提供了优秀的交互体验,开发人员只需利用平台提供的接口数据写入工具以及简单的点击操作就可以实现接口的管理.免费 ...
- Cutting Game(POJ 2311)
原题如下: Cutting Game Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 5721 Accepted: 208 ...
- oracle之三资源管理
Oracle 资源管理 12.1 为什么要使用Oracle资源管理器 传统意义上,系统的资源分配是由OS来完成的,但是对于数据库资源,OS分配资源会带来一些问题: 以Linux为例,最为突出的一个问题 ...
- ctfhub sql注入 整数型注入
整数型注入 手工注入 1.查看是否存在sql注入,及sql注入类型 2.确定列数 3.确定注入点,以及数据库版本,数据库名称 4.查表名 5.查字段名以及flag值 获得flag值 sqlmap做法 ...
- [LeetCode]67. 二进制求和(字符串)(数学)
题目 给你两个二进制字符串,返回它们的和(用二进制表示). 输入为 非空 字符串且只包含数字 1 和 0. 题解 两个字符串从低位开始加,前面位不够补0.维护进位,最后加上最后一个进位,最后反转结果字 ...
