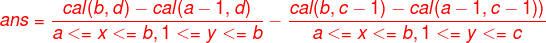BZoj 2301 Problem b(容斥定理+莫比乌斯反演)
2301: [HAOI2011]Problem b
Time Limit: 50 Sec Memory Limit: 256 MB
Submit: 7732 Solved: 3750
[Submit][Status][Discuss]
Description
对于给出的n个询问,每次求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y) = k,gcd(x,y)函数为x和y的最大公约数。
100%的数据满足:1≤n≤50000,1≤a≤b≤50000,1≤c≤d≤50000,1≤k≤50000
Input
第一行一个整数n,接下来n行每行五个整数,分别表示a、b、c、d、k
Output
共n行,每行一个整数表示满足要求的数对(x,y)的个数
Sample Input
2
2 5 1 5 1
1 5 1 5 2
Sample Output
14
3
题解:简化为计算a/k<=x<=b/k,c/k<=y<=d/k满足gcd(x,y)=1的x,y有多少对;cal(n,m)代表1<=x<=n,1<=y<=m满足gcd(x,y)=1的(x,y)对数,则根据容斥定理:
#include<iostream>
#include<stdio.h>
#define ll long long
using namespace std;
const ll N=50007;
ll prime[N],mu[N];
bool mark[N];
void getmu()
{
mu[1]=1;
int cnt=0;
for(int i=2;i<=N;i++){
if(!mark[i])
prime[cnt++]=i,mu[i]=-1;
for(int j=0;j<cnt&&i*prime[j]<=N;j++){
mark[i*prime[j]]=1;
if(i%prime[j]){
mu[i*prime[j]]=-mu[i];
}else{
mu[i*prime[j]]=0;break;
}
}
mu[i]+=mu[i-1];//后面不会再用到mu[i],所以可以直接记为前缀和
}
}
ll cal(ll n,ll m){
if(n>m)
swap(n,m);
ll ans=0;
for(ll l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(mu[r]-mu[l-1])*(n/l)*(m/l);
}
return ans;
}
int main()
{
int T;
ll a,b,c,d,k;
getmu();
scanf("%d",&T);
while(T--){
scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
a=(a-1)/k,b=b/k,c=(c-1)/k,d=d/k;
printf("%lld\n",cal(b,d)-cal(a,d)-(cal(c,b)-cal(c,a)));
}
return 0;
}
BZoj 2301 Problem b(容斥定理+莫比乌斯反演)的更多相关文章
- HDU 1695 GCD 欧拉函数+容斥定理 || 莫比乌斯反演
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- BZOJ 2005 [Noi2010]能量采集 (数学+容斥 或 莫比乌斯反演)
2005: [Noi2010]能量采集 Time Limit: 10 Sec Memory Limit: 552 MBSubmit: 4493 Solved: 2695[Submit][Statu ...
- 【容斥原理,莫比乌斯反演】用容斥替代莫比乌斯反演第二种形式解决gcd统计问题
名字虽然很长.但是其实很简单,对于这一类问题基本上就是看你能不能把统计的公式搞出来(这时候需要一个会推公式的队友) 来源于某次cf的一道题,盼望上紫的我让潘学姐帮我代打一道题,她看了看跟我说了题解,用 ...
- hdu1695(容斥 or 莫比乌斯反演)
刚开始看题,想了一会想到了一种容斥的做法.复杂度O( n(3/2) )但是因为题目上说有3000组测试数据,然后吓尿.完全不敢写. 然后想别的方法. 唉,最近精神有点问题,昨天从打完bc开始想到1点多 ...
- 【CF900D】Unusual Sequences 容斥(莫比乌斯反演)
[CF900D]Unusual Sequences 题意:定义正整数序列$a_1,a_2...a_n$是合法的,当且仅当$gcd(a_1,a_2...a_n)=x$且$a_1+a_2+...+a_n= ...
- 洛谷P4318 完全平方数(容斥,莫比乌斯反演)
传送门 求第$k$个没有完全平方数因数的数 一开始是想筛一波莫比乌斯函数,然后发现时间复杂度要炸 于是老老实实看了题解 一个数的排名$k=x-\sum_{i=1}^{x}{(1-|\mu(i)|)}$ ...
- ZOJ 3868 GCD Expectation (容斥+莫比乌斯反演)
GCD Expectation Time Limit: 4 Seconds Memory Limit: 262144 KB Edward has a set of n integers {a1 ...
- BZOJ2839 : 集合计数 (广义容斥定理)
题目 一个有 \(N\) 个 元素的集合有 \(2^N\) 个不同子集(包含空集), 现在要在这 \(2^N\) 个集合中取出若干集合(至少一个), 使得它们的交集的元素个数为 \(K\) ,求取法的 ...
- 【莫比乌斯反演】关于Mobius反演与gcd的一些关系与问题简化(bzoj 2301 Problem b&&bzoj 2820 YY的GCD&&BZOJ 3529 数表)
首先我们来看一道题 BZOJ 2301 Problem b Description 对于给出的n个询问,每次求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y) = k,gcd( ...
随机推荐
- classpath和classpath*的区别
classpath 指的是自己项目里的编译后的class路径 classpath* 包含jar包里面的class路径
- ovs常用操作
1.添加网桥:ovs-vsctl add-br 交换机名 2.删除网桥:ovs-vsctl del-br 交换机名 3.添加端口:ovs-vsctl add-port 交换机名 端口名(网卡名) 4. ...
- [转] 多核CPU 查看进程分配的CPU具体核id
转自:https://linux.cn/article-6307-1.html ps. 方法二简明直接 done! 当你在 多核 NUMA 处理器上运行需要较高性能的 HPC(高性能计算)程序或非常消 ...
- Python3学习笔记33-正则表达式
学习文章传送门 正则表达式是用来匹配字符串的.只要符合规则的字符串.就可以认为匹配了.否则,这个字符串不合法. \d:可以匹配一个数字 ‘00\d’可以匹配001不能匹配00A \w:可以匹配 ...
- vc++基础班[26]---进程的相关操作
①.ShellExecute 进行进程的创建,属于 shell api: //int iRet = (int)ShellExecute(m_hWnd, _T("open"), ...
- P3203 [HNOI2010]弹飞绵羊 —— 懒标记?分块?
好久没写博客了哈,今天来水一篇._(:з」∠)_ 题目 :弹飞绵羊(一道省选题) 题目描述 某天,Lostmonkey发明了一种超级弹力装置,为了在他的绵羊朋友面前显摆,他邀请小绵羊一起玩个游戏.游戏 ...
- MySQL查询语句练习题,测试基本够用了
Sutdent表的定义 字段名 字段描述 数据类型 主键 外键 非空 唯一 自增 Id 学号 INT(10) 是 否 是 是 是 Name 姓名 VARCHAR(20) 否 否 是 否 否 Sex 性 ...
- java结合testng,利用txt做数据源的数据驱动实例
import org.testng.annotations.DataProvider; import org.testng.annotations.Test; import java.io.Buffe ...
- Spring Cloud源码分析(四)Zuul:核心过滤器
通过之前发布的<Spring Cloud构建微服务架构(五)服务网关>一文,相信大家对于Spring Cloud Zuul已经有了一个基础的认识.通过前文的介绍,我们对于Zuul的第一印象 ...
- ssh: connect to host github.com port 22: Connection timed out
问题描述 $ git clone git@github.com:MaugerWu/MaugerWu.github.io.git Cloning into 'MaugerWu.github.io'... ...