非负矩阵分解（4）：NMF算法和聚类算法的联系与区别

作者：桂。

时间：2017-04-14   06:22:26

链接：http://www.cnblogs.com/xingshansi/p/6685811.html

声明：欢迎被转载，不过记得注明出处哦~

---

前言

之前梳理了一下非负矩阵分解（Nonnegative matrix factorization, NMF），主要有：

　　1）准则函数及KL散度

　　2）NMF算法推导与实现

　　3）拉格朗日乘子法求解NMF（将含限定NMF的求解 一般化）

谱聚类可以参考之前的文章：

　　1）拉普拉斯矩阵（Laplace Matrix）与瑞利熵（Rayleigh quotient）

　　2）谱聚类（Spectral clustering）（1）：RatioCut

　　3）谱聚类（Spectral clustering）（2）:NCut

总感觉NMF跟聚类有联系，这里试着从聚类角度分析一下非负矩阵分解，主要包括：

　　1）Kmeans与谱聚类

　　2）对称非负矩阵分解（symmetric NMF，SyNMF）;

　　3）非对称非负矩阵分解;

内容为自己的学习总结，如果有不对的地方，还请帮忙指出。文中多有借鉴他人的地方，最后一并给出链接。

一、Kmeans与谱聚类

　　A-Kmeans定义

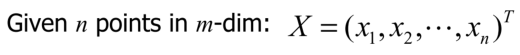，准则函数为：

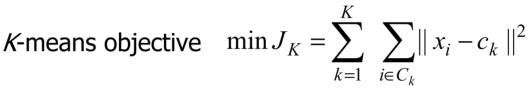
可以重写为：

定义h：

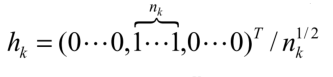
$n_k$为第k类样本的个数，则准则函数变为：

从而Kmeans的优化问题，等价于：

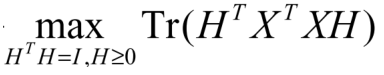
　　B-Kmeans与谱聚类（Spectral clustering）的联系

上文给出了h的定义：

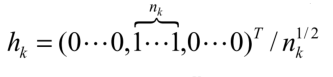
回顾谱聚类中RatioCut定义h的思路：

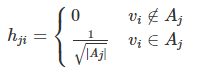
回顾RatioCut求解问题：

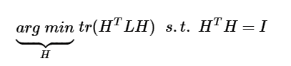
可以看出求解的思路完全一致，不同的是RatioCut是拉普拉斯矩阵L，而Kmeans是矩阵$X^TX$。正因为这点不同，Kmeans在利用谱聚类的思路求解时，略有差别。利用Kmeans的思想求Kmeans，听着这不是欠揍吗？ 这里只是为了分析谱聚类一般方法（L）与谱聚类对应的Kmeans（$X^TX$）二者的不同。

再次写出RatioCut的步骤：

步骤一：求解拉普拉斯矩阵L

步骤二：对L进行特征值分解，并取K个最小特征值对应的特征向量（K为类别数目）

步骤三：将求解的K个特征向量（并分别归一化），构成新的矩阵，对该矩阵进行kmeans处理

kmeans得到的类别标签，就是原数据的类别标签，至此完成RatioCut聚类。

对应Kmeans呢？是不是把$X^TX$换成L就等价于对原数据Kmeans?

步骤一：求解$X^TX$

步骤二：对$X^TX$进行特征值分解，并取K个最大特征值对应的特征向量（K为类别数目）

步骤三：将求解的K个特征向量（并分别归一化），构成新的矩阵，对该矩阵进行kmeans处理

kmeans得到的类别标签，就是原数据的类别标签，至此完成RatioCut聚类。

对应测试code:

L = X'*X;% matrix
%%Step2:Eigenvalues decomposition
K = 3;
[Qini,V] = eig(L);
%%Step3:New matrix Q
[~,pos] = sort(diag(V),'ascend');
Q = Qini(:,pos(1:K));
Q = Q./repmat(sqrt(diag(Q'*Q)'),N,1);
[idx,ctrs] = kmeans(Q,K);

我们可以利用数据测试一下：

再来看看直接对原数据Kmeans的结果：

利用谱聚类的思想求解，得出了错误的分类结果，而直接Kmeans效果是理想的。

原因何在？问题就出在矩阵L上。回顾之前提到的拉普拉斯矩阵L特性：

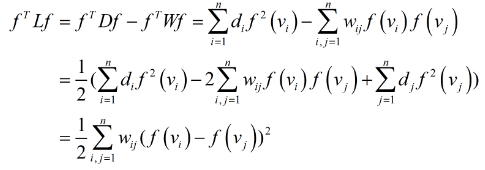
它表示的是不同数据点特征的差距，而$X^TX$呢？

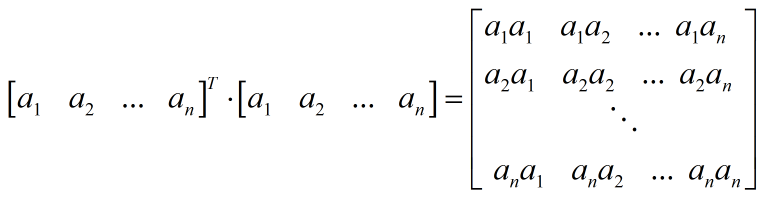
更像是一种余弦距离的测度，普通的Kmeans自然不能很好解决聚类。其实对$X^TX$利用谱聚类，特征向量子空间是严谨的，以三类为例，将特征子空间投影到二维，如下图中间所示，很容易看出子空间特征是分成三类的，但聚类之后呢？如右图所示，就出现了判别错误。这也是为什么上面两种结果不一致。

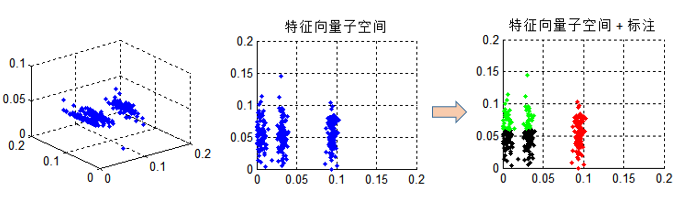
总而言之：Kmeans是与谱聚类的思想一致，但由于中间矩阵不同，二者思路略有差异。

 　　C-Kernel Kmeans与谱聚类

这里就再啰嗦一下，数据分类效果不理想，映射到高维呢？也就是核函数（Kernel function）的思想。

重新写出谱聚类框架下的Kmeans：

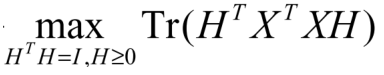
对X进行映射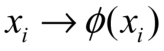：，得出核函数下的Kmeans(Kernel Kmeans)

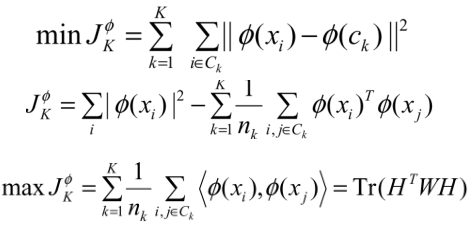
重新给出code(以kernel 取gaussian为例):

%Kmeans
sigma2 = .02;
L = exp(-dist(X,X').^2*sigma2);
[Qini,V] = eig(L);
%%Step3:New matrix Q
[~,pos] = sort(diag(V),'descend');
Q = Qini(:,pos(1:K));
for i =1:K
    Q(:,i) = Q(:,i)-min(Q(:,i));
end
Q = Q./repmat(sqrt(diag(Q'*Q)'),K*N,1);
[idx,ctrs] = kmeans(Q,K);

　　对应分类结果：

这个时候分类就理想了。

二、对称非负矩阵分解（SyNMF）

　　A-原理介绍

Kmeans与RatioCut的理论框架是统一的，其实准则函数等价为：

现在将$H^TH = I$的约束去掉，泛化后的求解问题为：

这就是对称非负矩阵分解（SyNMF）的思路。

　　B-算法求解

求解思路还是利用拉格朗日乘子+KKT，不再细说，给出结果：

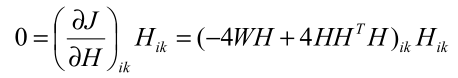
泛化后：

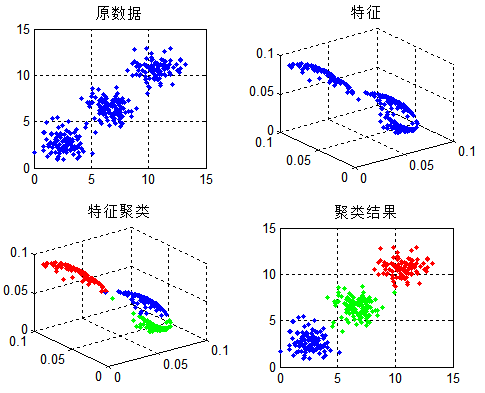
得到H之后，如何实现数据的label判别？

可以看出得到的H分为三类，对应三种label, 即可实现数据分离。

给出SymNMF与谱聚类的对比：

对应的code可以点击这里。

给出一个测试结果图，测试数据为三类：

三、非对称非负矩阵分解

SymNMF是Spectral clustering的泛化推广。

上文分析的是对称的谱聚类问题：

• Spectral clustering

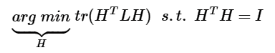
• SymNMF

同样的方式，分析非对称的谱聚类问题：

• Spectral clustering

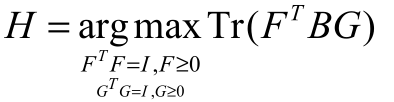
该问题可以转化为：

同样的，对于：

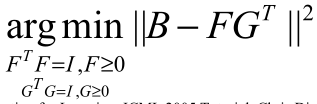
进行泛化：

这就是NMF的准则函数，即：

• NMF

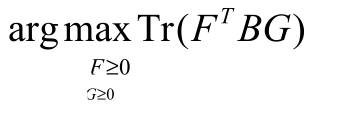
现在来总结一下：

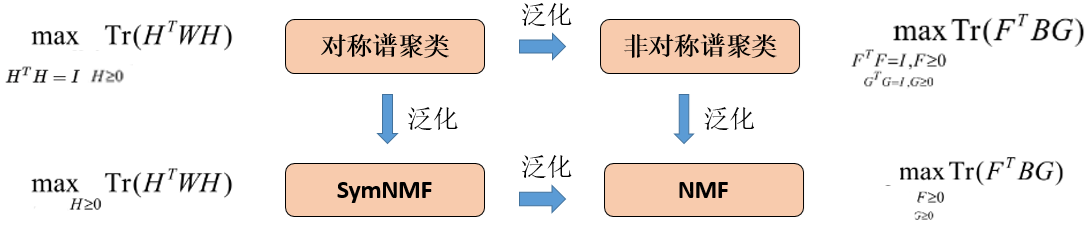
关系是不是一目了然了？如何添加更多约束项呢？比如希望H矩阵尽可能系数等等，就在上面这几类问题的准则函数后添加约束，转化成对偶问题求解即可。

题外话

　　A-非负矩阵NMF实现数据聚类

分析了这么多，已经解开了之前的困惑：谱聚类与NMF之间的联系。

回顾上面分析Kmeans提到的三类数据聚类问题，对$XX^T$进行NMF处理：

更直观地，将数据放在对应维度观察：

可以看到，由于矩阵对称，即figure对称，对W/H聚类，都可以得到三类标签，从而实现数据的聚类。对于非对称呢？自然想到：如果W对应样本数量维度，则对W进行聚类，如果H对应样本数量维度，就对H进行聚类，同样可以实现数据聚类。

给出一个利用（Kernel kmeans）聚类以及利用NMF聚类的对比示例。

利用$X^TX$是kmeans的思路，利用$L$是RatioCut思路，事实上，泛化之后，直接利用$X^TX$也可以利用是NMF的思路。

　　

clc;clear all;close all;
N = 100;
K = 3;
X = [randn(N,2)+ones(N,2);...
    randn(N,2)+3*ones(N,2);...
    randn(N,2)-4*ones(N,2)];
posran = randperm(K*N);
X = X-min(min(X));
X = X(posran,:);
 
%%方法一 基于Data: 利用 XX'  + 核心函数
sigma2 = 0.02;
L = exp(-dist(X,X')*sigma2);
%%Step2:Eigenvalues decomposition
[Qini,V] = eig(L);
%%Step3:New matrix Q
[~,pos] = sort(diag(V),'descend');
Q = Qini(:,pos(1:K));
for i =1:K
    Q(:,i) = Q(:,i)-min(Q(:,i));
end
Q = Q./repmat(sqrt(diag(Q'*Q)'),K*N,1);
[idx,ctrs] = kmeans(Q,K);
figure
subplot 221
plot(X(:,1),X(:,2),'.');
title('原数据');grid on;
subplot 222
plot3(Q(:,1),Q(:,2),Q(:,3),'b.');
title('特征');grid on;
subplot  223
plot3(Q(idx==1,1),Q(idx==1,2),Q(idx==1,3),'b.');hold on;
plot3(Q(idx==2,1),Q(idx==2,2),Q(idx==2,3),'r.');hold on;
plot3(Q(idx==3,1),Q(idx==3,2),Q(idx==3,3),'g.');hold on;
title('特征聚类');grid on;
subplot 224
plot(X(idx==1,1),X(idx==1,2),'b.');hold on;
plot(X(idx==2,1),X(idx==2,2),'r.');hold on;
plot(X(idx==3,1),X(idx==3,2),'g.');hold on;
title('聚类结果');grid on;
%%方法2 基于NMF: 对X*X'聚类
%即NMF
Iter = 500;
K = 3;
[W,H] = nmf(X*X',K,Iter);
[idx,ctrs] = kmeans(W,K,'distance','cityblock');
figure
subplot 221
plot(X(:,1),X(:,2),'.');
title('原数据');grid on;
subplot 222
plot3(W(:,1),W(:,2),W(:,3),'b.');
title('W矩阵');grid on;
subplot  223
plot3(W(idx==1,1),W(idx==1,2),W(idx==1,3),'b.');hold on;
plot3(W(idx==2,1),W(idx==2,2),W(idx==2,3),'r.');hold on;
plot3(W(idx==3,1),W(idx==3,2),W(idx==3,3),'g.');hold on;
title('W矩阵聚类');grid on;
subplot 224
plot(X(idx==1,1),X(idx==1,2),'b.');hold on;
plot(X(idx==2,1),X(idx==2,2),'r.');hold on;
plot(X(idx==3,1),X(idx==3,2),'g.');hold on;
title('聚类结果');grid on;

　　这里的代码只是为了说明理论问题，代码本身不足以支持应用。给出对应结果图：

基于$X^TX$的Kmeans:

基于$X^TX$的NMF:

事实上，直接对$X$进行NMF聚类，只要将$X^TX$替换为$X$即可，对应结果图：

这里可以理解为：H是对应的字典信息，W是线性变换。

　　B-图的聚类（不再是数据的聚类）

上文分析的是对数据点进行分类，如果直接对邻接矩阵、拉普拉斯矩阵，也就是图片信息进行分类呢？（可能有点绕，但数据点聚类，并不代表图就是聚类，图明显可以聚类，对应的数据点也未必可以聚类）。

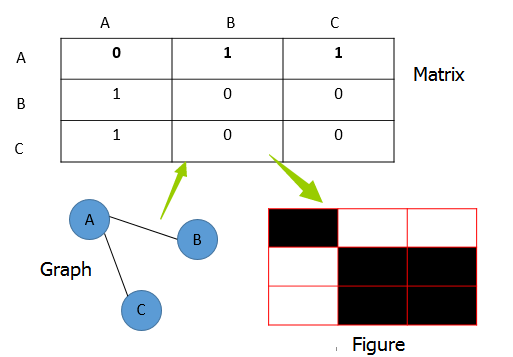
图对应的矩阵，如拉普拉斯矩阵、邻接矩阵等等，说到底都是figure的表达，如上图所示，因此上文分析的矩阵W/B，可以用图片的信息替代。

对于图的聚类，一种思路是将图中像素点读取，转化成数据格式，再进行聚类。

Data角度就是前面分析的种种类型，Figure角度呢？

给出NMF对图片的处理结果（分四类）：

对应code:

img = imread('2.png');
V = 1-im2bw(rgb2gray(img));
figure
K = 4;
Iter = 500;
[W,H] = nmf(V, K, Iter);
subplot 331
mesh(V);
title('原数据')
 
for i =1:K
    subplot(3,3,i+1);
    mesh(W(:,i)*H(i,:));
    title(['分解',num2str(i)])
end

NMF对于Figure是一种线性表达的思路，可以分离的基础是数据不共线（横/纵），再给出之前音乐分离的语谱图：

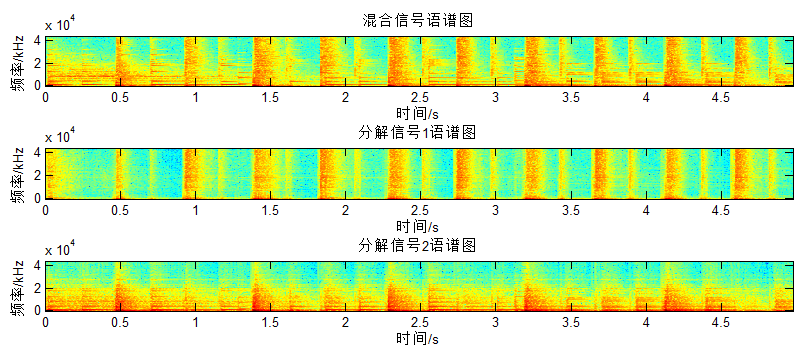
之所以可以分离正是因为音乐频谱的周期性，所以对于非周期的说话人，直接应用NMF应该是无效的，对应的时域波形：

参考：

• On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering
• Symmetric Nonnegative Matrix Factorization for Graph Clustering