【CF838E】 Convex Countour

【CF838E】 Convex Countour

首先观察题目的性质

由于是凸包，因此不自交路径中的一条边\((x, y)\)的两端点只能向与\(x\)或\(y\)相邻的结点连边。

举个栗子，若选取了一条边\((x, y)\)，且假设编号从\(x\)到\(y\)结点已经在一条不自交路径中（不考虑特殊情况），那么向外扩展路径只能连向相邻的点，即只能连边\((x+1, y)\)或\((x, x+1)\)或\((x, y-1)\)或\((y-1, y)\)

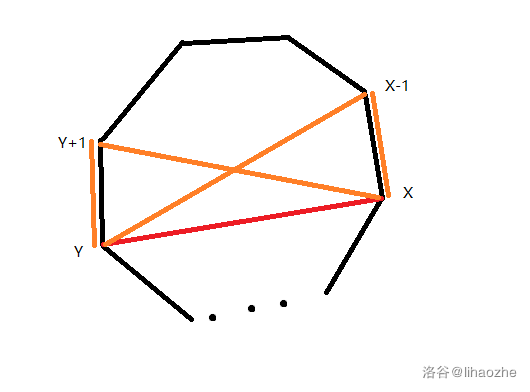
很容易用反证法证明。假设连边\((x-2, y)\)，那么点\(x-1\)则无法通过一条不与\((x, y)\)或\((x-2, y)\)相交的路径与其他点连通。而此题路径要覆盖所有点，即所有点之间连通，则矛盾。因此上述结论成立。

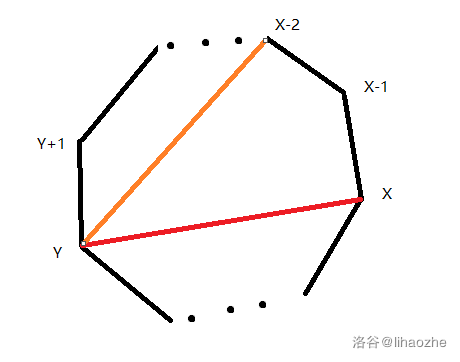
由于选取的路径每次只能向外扩展一个点，那么此题就变成了区间动态规划问题。

设\(f_{l, r, 0/1}\)表示区间\([l, r]\)的最长路径长度，\(0\)表示路径终点在\(l\)， \(1\)表示路径终点在\(r\)。

那么可以得到

\[f_{l, r, 0}=max\{f_{l+1, r, 0}+dis(l, l+1), f_{l+1, r, 1}+dis(l, r)\}\\f_{l, r, 1}=max\{f_{l, r-1, 0}+dis(r, l), f_{l, r-1, 1}+dis(r, r-1)\}
\]

且易知\(f_{x, x, 0}=f_{x, x, 1}=0\)

此题卡空间，不能开两倍大小，将下标取模后再dp即可

代码如下

#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;

const int N=2510;
struct Point {
	double x, y;
	Point(int x=0, int y=0):x(x), y(y){}
} p[N];
double dis(Point a, Point b) {
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double f[N][N][2];
int n;

int main() {
	scanf("%d", &n);
	for (int i=0; i<n; i++) {
		int x, y; scanf("%d%d", &x, &y);
		p[i]=Point(x, y);
	}
	for (int len=2; len<=n; len++)
		for (int l=0; l<n; l++) {
			int r=(l+len-1)%n;
			f[l][r][0]=max(f[(l+1)%n][r][0]+dis(p[l], p[(l+1)%n]), f[(l+1)%n][r][1]+dis(p[l], p[r]));
			f[l][r][1]=max(f[l][(r-1+n)%n][0]+dis(p[r], p[l]), f[l][(r-1+n)%n][1]+dis(p[r], p[(r-1+n)%n]));
		}
	double ans=0;
	for (int i=0; i<n; i++) ans=max(ans, max(f[i][(i+n-1)%n][0], f[i][(i+n-1)%n][1]));
	printf("%.10lf", ans);
	return 0;
}