B+树索引结构解析
一、二分查找法
二分查找法(binary search)也成为折半查找法。用来查找一组有序的记录组中的某一记录。
基本思想是:将记录按有序化(递增或递减)排列,在查找过程中采用跳跃式方法查找,即先以有序数列的中点位置为比较对象,如果要找的元素值小于该中点元素,则将待查询列缩小为左半部分,否则为右半部分。通过一次比较,将查询区间缩小一半。
如有5,10,19,21,31,37,42,48,50,52这10个数,要查48这个数,其查找过程:
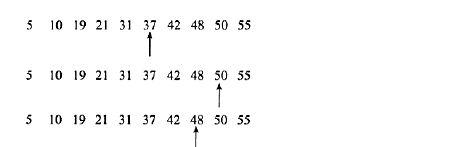
从图看,用了3次就找到了48这个数。如果是顺序查找,则需要8次,因此二分查找法的效率比顺序查找法要好(平均)。但是如果要查5这个数,顺序查只需1次,而二分查找需要4次。
对于上面的10个数来说,平均查找次数为(1+2+3+4+5+6+7+8+9+10)/10=5.5次。而二分查找为(4+3+2+4+3+1+4+3+2+3)/10=2.9次。
在最坏的情况下,顺序查找的次数为10,而二分查找法为4
二、二叉查找树和平衡二叉树
B+树是通过二叉查找树,再由平衡二叉树,B树演化而来。
二叉查找树中定义:左子树的键值总是小于根的键值,右子树的键值总是大于根的键值。因此可以通过中序遍历得到键值的排序输出
若想最大性能的构造一颗二叉查找树,需要这颗二叉查找树是平衡,从而引出了新的定义-----平衡二叉树,或称为AVL树。
平衡二叉树定义:首先复合二叉查找树的定义,其次必须满足任何节点的两个子树的高度最大差为1.
平衡二叉树的查询速度很快,但是维护一颗平衡二叉树的代价很大,通常来说,需要1次或多次左旋和右旋来得到插入或更新后树的平衡性。如下所示:
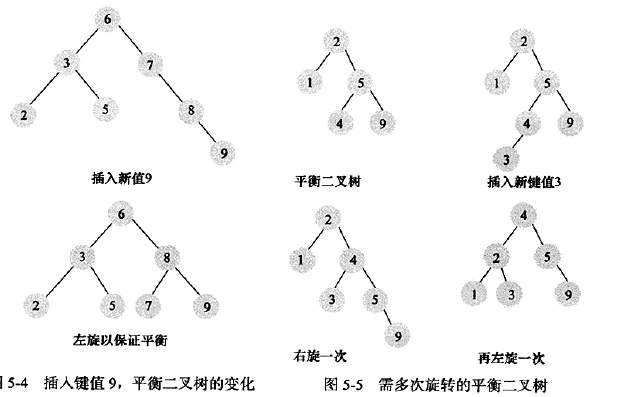
三、B+树
B+树和二叉树、平衡二叉树一样都是经典的数据结构。
B+树由B树和索引顺序访问方法(ISAM,这就是MyISAM引擎最初参考的数据结构)演化而来,实际中已经没有使用B树的情况了。
B+树是为磁盘或其他直接存储辅助设备设计的一种平衡查找时。
B+树中,所有记录节点都是按键值的大小顺序存放在同一层的叶子节点上,由各叶子节点指针进行连接。
如下:其高度为2,每页存放4条记录,扇出(fan out)为5。所有记录都在叶子节点上,并且是顺序存放的。
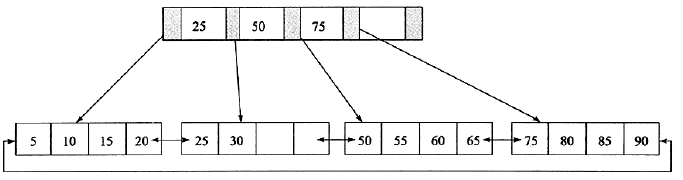
四、B+树的插入操作
B+树的插入必须保证插入后叶子节点中的记录依然排序,同时需要考虑插入到B+树的三种情况,每种情况都会导致不同的插入算法。如下所示:
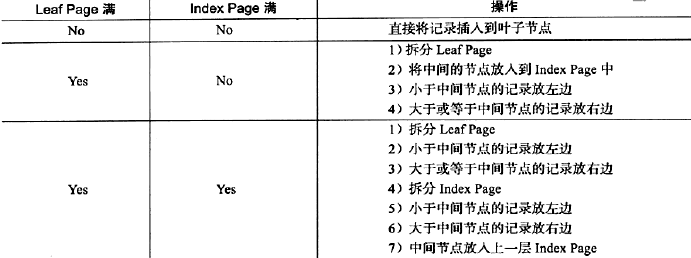
1、如下图这颗B+树,若用户插入28这个值,发现当前叶子页leafPage和IndexPage索引页都没有满,直接插入就行。
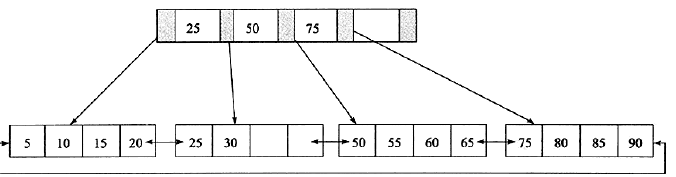
图(1)
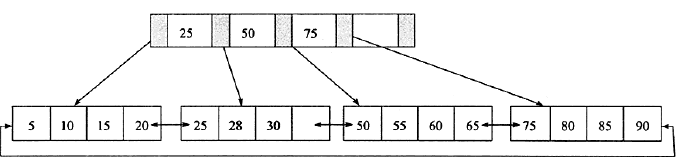
图(2)
2、从上图接着插入70这个键值,这时原来的leafPage已经满了,但是IndexPage还没有。这时插入leafPage后的情况为50、55、60、65、70,并根据中间值60来拆分叶子节点,可得下图。
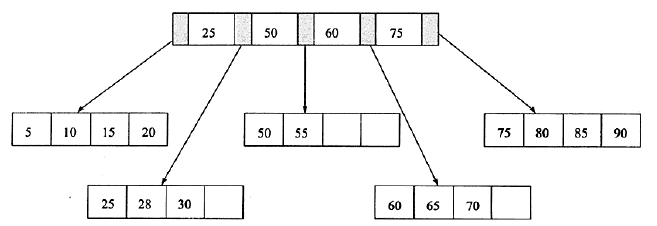
图(3)
为了保持平衡对于新插入的键值可能需要做大量的拆分页(split)操作。因为B+树结构主要用于磁盘,也拆分意味着磁盘操作,所以应该在可能的情况下尽量减小页的拆分操作。因此B+树会提出平衡二叉树的旋转(Rotation)功能。
旋转发生在leafPage已满,但是其左右兄弟节点没有满的情况下。这时B+树不会急于去拆分页操作,而是将记录移到所在页的兄弟页节点上,通常情况下,左兄弟会被首先检查用来做旋转操作。若如此,插入70应该左旋为:

图(4)
3、最后插入95,这时复合第三种情况,即leafPage和IndexPage都满了,这时需要做两次拆分
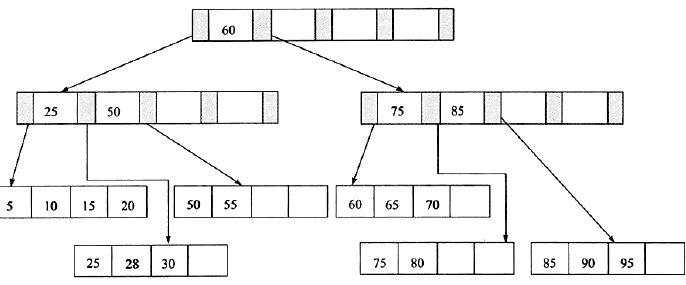
图(5)
五、B+树的删除操作
B+树使用填充因子(fill factor)来控制树的删除变化,50%是填充因子可设的最小值。
B+树的删除操作同样必须保证删除后叶子节点中的记录依然排序,同插入一样,B+树删除操作同样需要考虑以下三种情况:

1、根据图(5)的B+树来进行删除。首先删除键值为70的记录:
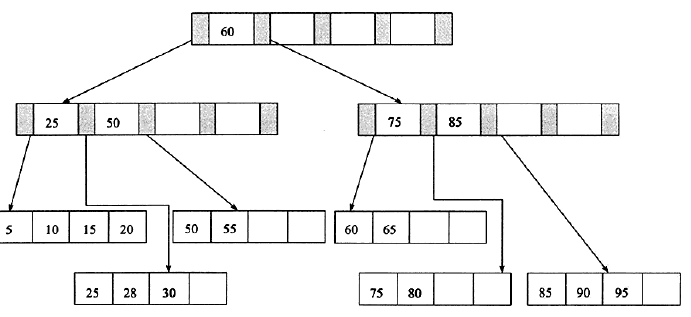
接着删除键值为25的记录,但是该值还是IndexPage中的值,因此在删除LeafPage中的25后,还应将25的右兄弟节点28更新到PageIndex中,如图:

最后删除60这个键值。删除LeafPage中键值为60的记录后,Fill Factor小于50%,这时需要做合并操作,同样,在删除IndexPage中相关记录后需要做IndexPage的合并操作。
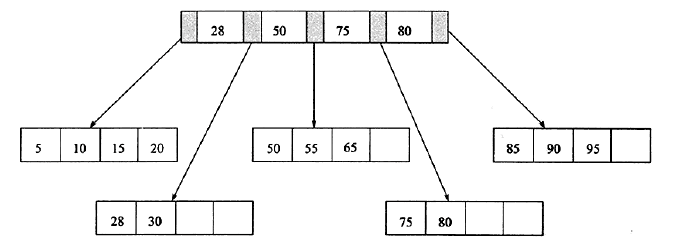
B+树索引结构解析的更多相关文章
- Oracle索引梳理系列(二)- Oracle索引种类及B树索引
版权声明:本文发布于http://www.cnblogs.com/yumiko/,版权由Yumiko_sunny所有,欢迎转载.转载时,请在文章明显位置注明原文链接.若在未经作者同意的情况下,将本文内 ...
- B+树索引和哈希索引的区别——我在想全文搜索引擎为啥不用hash索引而非得使用B+呢?
哈希文件也称为散列文件,是利用哈希存储方式组织的文件,亦称为直接存取文件.它类似于哈希表,即根据文件中关键字的特点,设计一个哈希函数和处理冲突的方法,将记录哈希到存储设备上. 在哈希文件中,是使用一个 ...
- 浅谈B+树索引的分裂优化(转)
http://www.tamabc.com/article/85038.html 从MySQL Bug#67718浅谈B+树索引的分裂优化 原文链接:http://hedengcheng.com/ ...
- MySQL B+树索引和哈希索引的区别
导读 在MySQL里常用的索引数据结构有B+树索引和哈希索引两种,我们来看下这两种索引数据结构的区别及其不同的应用建议. 二者区别 备注:先说下,在MySQL文档里,实际上是把B+树索引写成了BT ...
- 从MySQL Bug#67718浅谈B+树索引的分裂优化(转)
原文链接:http://hedengcheng.com/?p=525 问题背景 今天,看到Twitter的DBA团队发布了其最新的MySQL分支:Changes in Twitter MySQL 5. ...
- B+树索引和哈希索引的区别[转]
导读 在MySQL里常用的索引数据结构有B+树索引和哈希索引两种,我们来看下这两种索引数据结构的区别及其不同的应用建议. 二者区别 备注:先说下,在MySQL文档里,实际上是把B+树索引写成了BTRE ...
- MySQL B+树索引和哈希索引的区别(转 JD二面)
导读 在MySQL里常用的索引数据结构有B+树索引和哈希索引两种,我们来看下这两种索引数据结构的区别及其不同的应用建议. 二者区别 备注:先说下,在MySQL文档里,实际上是把B+树索引写成了BTRE ...
- mysql索引是什么?索引结构和使用详解
索引是什么 mysql索引: 是一种帮助mysql高效的获取数据的数据结构,这些数据结构以某种方式引用数据,这种结构就是索引.可简单理解为排好序的快速查找数据结构.如果要查“mysql”这个单词,我们 ...
- [转帖]B树索引、位图索引和散列索引
B树索引.位图索引和散列索引 https://blog.csdn.net/huashanlunjian/article/details/84460436 索引在数据结构上可以分为三种B树索引.位图 ...
随机推荐
- Windows 好用的护眼软件
目录 1. 按 2. Windows10自带夜间模式 3. Iris Pro 3.1. 介绍 3.1.1. 保护用眼,改善睡眠 3.1.2. ×9 种不同的预设搭配 3.1.3. 计时器 3.1.4. ...
- linux创建相关待同步目录
[root@rsync-server-1 ~]# mkdir /data/{web,web_data}/redhat.sx -p [root@rsync-server-1 ~]# tree /data ...
- 调整notepad++的行距的方法
notepad++是一款免费开源的文本编辑器,在windows平台上表现非常好,可以自定义的地方多,还支持主题导入,导出和切换,对各种语言的语法高亮支持也是在各大文本编辑器中名列前茅,插件库的内容也非 ...
- lvm分区创建和扩容
shell> fdisk /dev/xvdb #### 选择磁盘 Command (m for help): m #### 帮助 Command action a toggle a bootab ...
- gcc的-D,-w,-W,-Wall,-O3这些参数的意义
一.-D 其意义是添加宏定义,这个很有用. 当你想要通过宏控制你的程序,不必傻乎乎的在程序里定义,然后需要哪个版本,去修改宏. 只需要在执行gcc的时候,指定-D,后面跟宏的名称即可. 示例: gcc ...
- hive之wordcount
1.创建一张表,记录文件数据,使用换行符作为分隔符 create table file_data(content string) row format delimited fields termina ...
- macOS gcc g++ c++ cc
安装完Xcode之后,系统中默认的编译器不再是Gcc系列,编译一些库的时候经常产生问题. 在PATH变量中设置symbol link,把gcc,g++,c++,cc全链接到Gcc系列.
- 【Java】commons-lang3中DateUtils类方法介绍
添加commons-lang3的Maven依赖 <dependency> <groupId>org.apache.commons</groupId> <art ...
- Ponds
Ponds Time Limit: 1500/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)Total Sub ...
- Milking Grid poj2185
Milking Grid POJ - 2185 时限: 3000MS 内存: 65536KB 64位IO格式: %I64d & %I64u 提交 状态 已开启划词翻译 问题描述 Eve ...
