神经网络优化篇：详解动量梯度下降法（Gradient descent with Momentum）

动量梯度下降法

还有一种算法叫做Momentum，或者叫做动量梯度下降法，运行速度几乎总是快于标准的梯度下降算法，简而言之，基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新的权重。

例如，如果要优化成本函数，函数形状如图，红点代表最小值的位置，假设从这里（蓝色点）开始梯度下降法，如果进行梯度下降法的一次迭代，无论是batch或mini-batch下降法，也许会指向这里，现在在椭圆的另一边，计算下一步梯度下降，结果或许如此，然后再计算一步，再一步，计算下去，会发现梯度下降法要很多计算步骤对吧？

慢慢摆动到最小值，这种上下波动减慢了梯度下降法的速度，就无法使用更大的学习率，如果要用较大的学习率（紫色箭头），结果可能会偏离函数的范围，为了避免摆动过大，要用一个较小的学习率。

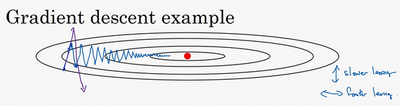
另一个看待问题的角度是，在纵轴上，希望学习慢一点，因为不想要这些摆动，但是在横轴上，希望加快学习，希望快速从左向右移，移向最小值，移向红点。所以使用动量梯度下降法，需要做的是，在每次迭代中，确切来说在第\(t\)次迭代的过程中，会计算微分\(dW\)，\(db\)，会省略上标\([l]\)，用现有的mini-batch计算\(dW\)，\(db\)。如果用batch梯度下降法，现在的mini-batch就是全部的batch，对于batch梯度下降法的效果是一样的。如果现有的mini-batch就是整个训练集，效果也不错，要做的是计算\(v_{{dW}}= \beta v_{{dW}} + \left( 1 - \beta \right)dW\)，这跟之前的计算相似，也就是\(v = \beta v + \left( 1 - \beta \right)\theta_{t}\)，\(dW\)的移动平均数，接着同样地计算\(v_{db}\)，\(v_{db} = \beta v_{{db}} + ( 1 - \beta){db}\)，然后重新赋值权重，\(W:= W -av_{{dW}}\)，同样\(b:= b - a v_{db}\)，这样就可以减缓梯度下降的幅度。

例如，在上几个导数中，会发现这些纵轴上的摆动平均值接近于零，所以在纵轴方向，希望放慢一点，平均过程中，正负数相互抵消，所以平均值接近于零。但在横轴方向，所有的微分都指向横轴方向，因此横轴方向的平均值仍然较大，因此用算法几次迭代后，发现动量梯度下降法，最终纵轴方向的摆动变小了，横轴方向运动更快，因此的算法走了一条更加直接的路径，在抵达最小值的路上减少了摆动。

动量梯度下降法的一个本质，这对有些人而不是所有人有效，就是如果要最小化碗状函数，这是碗的形状，画的不太好。

它们能够最小化碗状函数，这些微分项，想象它们为从山上往下滚的一个球，提供了加速度，Momentum项相当于速度。

想象有一个碗，拿一个球，微分项给了这个球一个加速度，此时球正向山下滚，球因为加速度越滚越快，而因为\(\beta\) 稍小于1，表现出一些摩擦力，所以球不会无限加速下去，所以不像梯度下降法，每一步都独立于之前的步骤，的球可以向下滚，获得动量，可以从碗向下加速获得动量。发现这个球从碗滚下的比喻，物理能力强的人接受得比较好，但不是所有人都能接受，如果球从碗中滚下这个比喻，理解不了，别担心。

最后来看具体如何计算，算法在此。

所以有两个超参数，学习率\(a\)以及参数\(\beta\)，\(\beta\)控制着指数加权平均数。\(\beta\)最常用的值是0.9，之前平均了过去十天的温度，所以现在平均了前十次迭代的梯度。实际上\(\beta\)为0.9时，效果不错，可以尝试不同的值，可以做一些超参数的研究，不过0.9是很棒的鲁棒数。那么关于偏差修正，所以要拿\(v_{dW}\)和\(v_{db}\)除以\(1-\beta^{t}\)，实际上人们不这么做，因为10次迭代之后，因为的移动平均已经过了初始阶段。实际中，在使用梯度下降法或动量梯度下降法时，人们不会受到偏差修正的困扰。当然\(v_{{dW}}\)初始值是0，要注意到这是和\(dW\)拥有相同维数的零矩阵，也就是跟\(W\)拥有相同的维数，\(v_{db}\)的初始值也是向量零，所以和\(db\)拥有相同的维数，也就是和\(b\)是同一维数。

最后要说一点，如果查阅了动量梯度下降法相关资料，经常会看到一个被删除了的专业词汇，\(1-\beta\)被删除了，最后得到的是\(v_{dW}= \beta v_{{dW}} +dW\)。用紫色版本的结果就是，所以\(v_{{dW}}\)缩小了\(1-\beta\)倍，相当于乘以\(\frac{1}{1- \beta}\)，所以要用梯度下降最新值的话，\(a\)要根据\(\frac{1}{1 -\beta}\)相应变化。实际上，二者效果都不错，只会影响到学习率\(a\)的最佳值。觉得这个公式用起来没有那么自然，因为有一个影响，如果最后要调整超参数\(\beta\)，就会影响到\(v_{{dW}}\)和\(v_{db}\)，也许还要修改学习率\(a\)，所以更喜欢左边的公式，而不是删去了\(1-\beta\)的这个公式，所以更倾向于使用左边的公式，也就是有\(1-\beta\)的这个公式，但是两个公式都将\(\beta\)设置为0.9，是超参数的常见选择，只是在这两个公式中，学习率\(a\)的调整会有所不同。

所以这就是动量梯度下降法，这个算法肯定要好于没有Momentum的梯度下降算法。