NgDL:第四周深层神经网络

4.3核对矩阵维数

根据前向的矩阵，可以计算出右上的规律，对于第L层的w来说，其维数为（n[L],n[L-1]），n[L]表示第L层的单元数。

4.4为什么深层神经网络会好用？

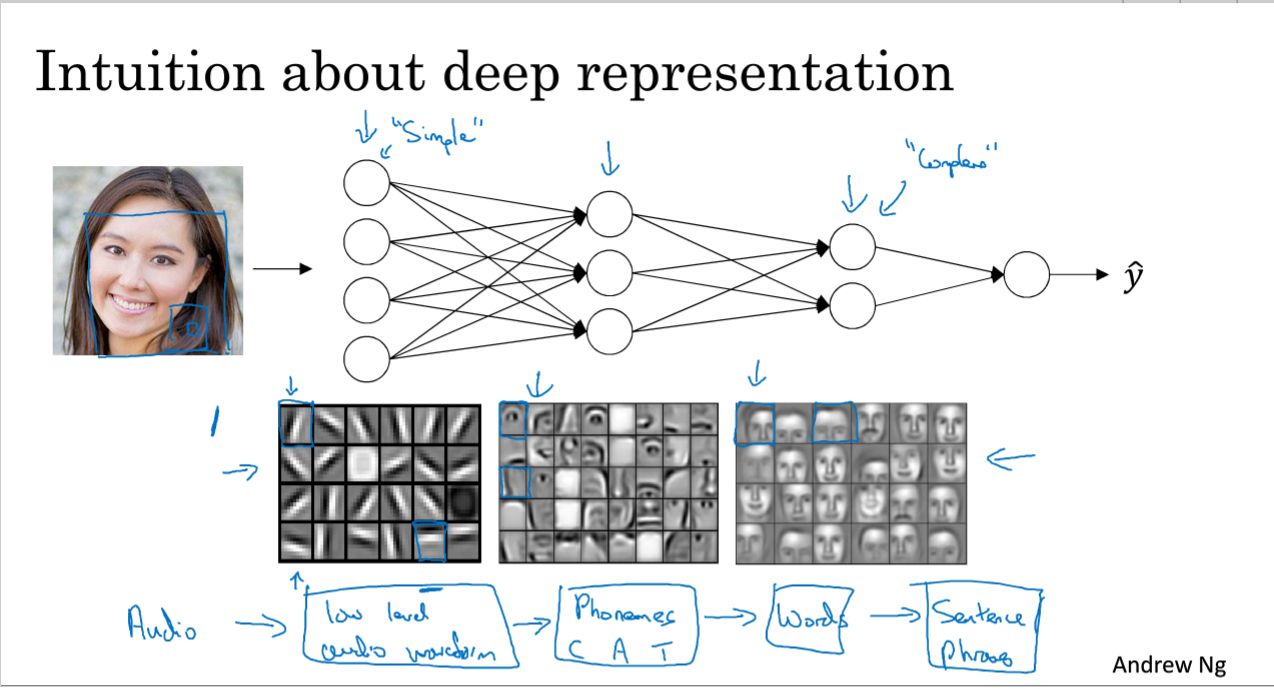
如果要做一个人脸识别的系统：那么浅层的神经网络，进行特征识别或边缘探测，第一张图中的一个小方块就是一个神经单元？无法理解。比如说有个神经单元去找眼睛的部分，这样每个神经元就可以找脸部不同的部位，最后将这些部分放在一起。

边缘探测中针对的都是比较小的，而到面部识别会针对较大的区域。金字塔形状的NN。

Ng讲到了在语音识别上的一个应用：

输入是一段音频，第一层神经网络可以探测比较低层次的音频波形特征，比如音调变高还是变低，然后可以去探测声音的基本单元（音位），cat中的“壳”就是一个音位，然后就可以识别单词，单词组合起来就是词组。

到网络深层时就可以做更复杂的事情，比如检测脸部或者词组。

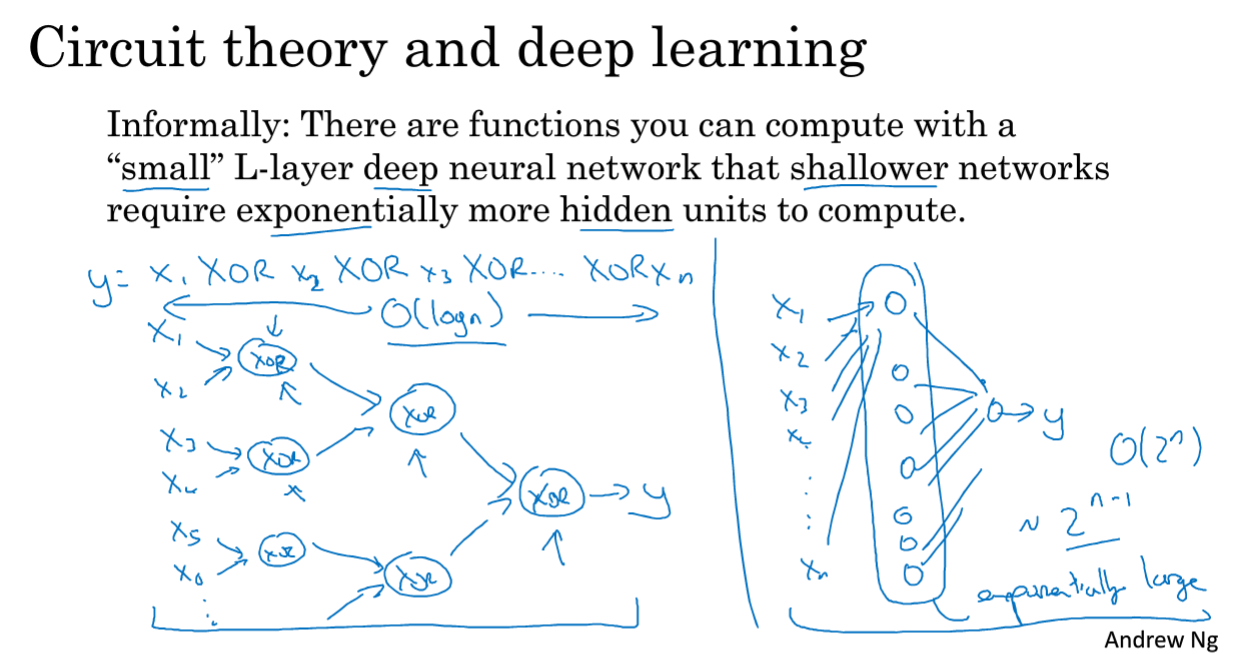
对于电路和深度学习的结合的例子说明为什么深度网络效果好。

假设要对输入特征计算异或，从x1 XOR....xn，如果画一个异或的树图，可建一个较深的异或树图，隐层数为log(n)，就是一个二叉树的高度；

如果不允许使用多层神经网络的话，只能使用一个隐层，那就需要考虑所有可能的组合，需要隐层单元数程指数式增长；（需要考虑所有的可能的结合情况？）

4.7参数VS超参数

参数：就是比如NN模型中的权重和偏执单元值。

超参数：就是能控制参数的参数。比如学习率α，迭代次数，隐含层层数、隐含层中的单元数、激活函数的选择

还有一些其他的超参数：momentum,minibatch size,正则化规则等。

//头一次知道超参数的定义，原来是这样，不过另外的超参数还不太明白。

这种公式表述的我还看不太懂，保留一下：