【HIHOCODER 1182】欧拉路·三

描述

---

小Hi和小Ho破解了一道又一道难题，终于来到了最后一关。只要打开眼前的宝箱就可以通关这个游戏了。

宝箱被一种奇怪的机关锁住：



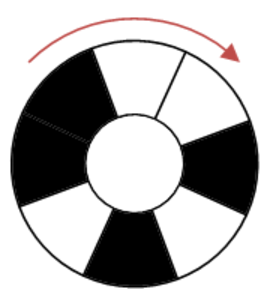
这个机关是一个圆环，一共有2^N个区域，每个区域都可以改变颜色，在黑白两种颜色之间切换。

小Ho控制主角在周围探索了一下，果然又发现了一个纸片：

机关黑色的部分表示为1，白色的部分表示为0，逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布，使得机关能够表示0~2^N-1所有的数字。

我尝试了很多次，终究没有办法打开，只得在此写下机关破解之法。

——By 无名的冒险者

小Ho：这什么意思啊？

小Hi：我给你举个例子，假如N=3，我们通过顺时针转动，可以使得正下方的3个区域表示为：



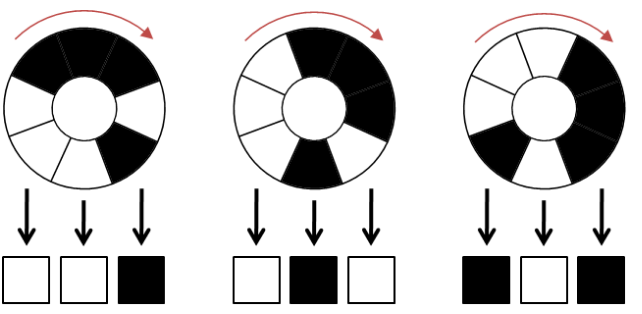
因为黑色表示为1，白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)

每转动一个区域，可以得到一个新的数字。一共可以转动2^{N次，也就是2}N个数字。我们要调整黑白区域的位置，使得这2^{N个数字恰好是0~2}N-1

小Ho：我懂了。若N=2，则将环上的黑白色块调整为"黑黑白白"，对应了"1100"。依次是"11","10","00","01"四个数字，正好是0~3。那么这个"黑黑白白"就可以打开机关了咯？

小Hi：我想应该是的。

小Ho：好像不是很难的样子，我来试试！

输入

---

第1行：1个正整数，N。1≤N≤15

输出

---

第1行：1个长度为2^N的01串，表示一种符合要求的分布方案

样例输入

3

样例输出

00010111

题解

可以把每k位二进制数看作一个点，它与左移一位+0和+1形成的新k位二进制数存在一条边相连。

这样只要每次不走重边，每次形成的都是一个新的数，这样走1<<n次，就可以生成0到1<<n -1的所有数字了

#include <bits/stdc++.h>
#define ll long long
#define inf 1000000000
#define PI acos(-1)
#define bug puts("here")
#define REP(i,x,n) for(int i=x;i<=n;i++)
#define DEP(i,n,x) for(int i=n;i>=x;i--)
#define mem(a,x) memset(a,x,sizeof(a))
using namespace std;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int N=(1<<15)+1;
bool vis[N];
int ans[N],tn,n;
bool euler(int u,int step){
    if(vis[u]) return false;
    if(step==tn+1) return true;
    ans[step]=u&1;
    vis[u]=true;
    if(euler((u<<1)&tn,step+1)) return true;
    if(euler((u<<1|1)&tn,step+1)) return true;
    vis[u]=false;
    return false;
}
int main(){
    n=read();
    tn=(1<<n)-1;
    euler(0,1);
    for(int i=1;i<n;i++)
		printf("0");
	for(int i=1;i<=tn-n+2;i++)
		printf("%d",ans[i]);
	return 0;
}