【bfs】最少转弯问题

题目描述

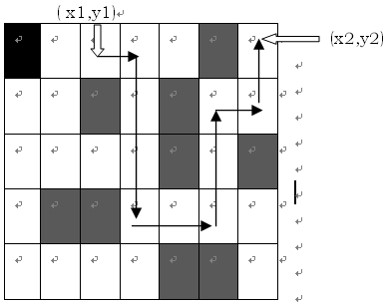
给出一张地图，这张地图被分为n×m（n,m<=100）个方块，任何一个方块不是平地就是高山。平地可以通过，高山则不能。现在你处在地图的（x1,y1）这块平地，问：你至少需要拐几个弯才能到达目的地（x2,y2）？你只能沿着水平和垂直方向的平地上行进，拐弯次数就等于行进方向的改变（从水平到垂直或从垂直到水平）的次数。例如：如图，最少的拐弯次数为5。

输入

第1行：n   m

第2至n+1行：整个地图地形描述（0：空地；1：高山），

如（图）第2行地形描述为：1 0 0 0 0 1 0

第3行地形描述为：0 0 1 0 1 0 0

……

第n+2行：x1  y1  x2  y2  （分别为起点、终点坐标）

输出

输出s （即最少的拐弯次数）

样例输入

5 7
1 0 0 0 0 1 0
0 0 1 0 1 0 0
0 0 0 0 1 0 1
0 1 1 0 0 0 0
0 0 0 0 1 1 0
1 3 1 7

样例输出

5

[思路]：

1.用bfs求，不过bfs要记录一下转弯次数，记得转弯时遇到大山或者是到边界

2.注意转弯时队首不用出

[注意]：linux下begin,end不能当变量！！！！！！

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<string>
#include<cstring>
using namespace std;
;
;
inline int read() {
    char c;
    ,f=;
    c=getchar();
    ') {
        if(c=='-') {
            f=-;
        }
        c=getchar();
    }
    ') {
        x=x*+c-';
        c=getchar();
    }
    return x*f;
 
}
 ]= {,,,-};
 ]= {,,-,};
struct node {
    int x,y,turn;
} strat,endddddddd,p;
queue<node> q;
][];
][];
int main() {
    memset(visit,,sizeof(visit));
    scanf("%d%d",&n,&m);
    ; i<=n; i++)
        ; j<=m; j++)
            scanf("%d",&a[i][j]);
    scanf("%d%d%d%d",&strat.x,&strat.y,&endddddddd.x,&endddddddd.y);
    q.push(strat);
    q.front().turn=;
    while(!q.empty()) {
        ; i<; i++) {
            p.x=q.front().x+dx[i];
            p.y=q.front().y+dy[i];
            &&p.x<=n&&p.y>&&p.y<=m&&!a[p.x][p.y]) {
                if(!visit[p.x][p.y]) {
                    if(p.x==endddddddd.x&&p.y==endddddddd.y) {
                        printf("%d\n",q.front().turn);
                        ;
                    }
                    visit[p.x][p.y]=;
                    p.turn=q.front().turn+;
                    q.push(p);
                }
                p.x+=dx[i];
                p.y+=dy[i];
            }
        }
        q.pop();
    }
}