深度学习中优化【Normalization】

深度学习中优化操作：

1. dropout
2. l1, l2正则化
3. momentum
4. normalization

1、为什么Normalization？

    深度神经网络模型的训练为什么会很困难？其中一个重要的原因是，深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。为了训好模型，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。

对于每一层网络得到输出向量的分布是不太有规律的，将这些没有规律的的输出结果放入激励层，会使得许多样本？因为偏离0坐标太远，而使得这些样本的值很大（等于1）或者很小（等于0），从而导致在反向传播时梯度消失。

我们在训练的时候希望每个batch在同一层网络下的输出结果是独立同分布的，这样能网络的泛化性就会比较强。

2、方式

1.Batch Normalization

BN的做法很简单，就是在输出结果在送到激励层之前，对输出结果做一次标准化。

前三步分别就是求均值与方差，并对其进行中心化，normalize中分母中的$\epsilon$,是为了避免除以0溢出。经过这三步，输出结果已经变成均值为$\mu _{b}$, 方差是$\sigma^{2}_{b}$的分布了。

最后一步非常重要。γ和β是可学习的，目的是让网络能够自己调节分布。我们获得一个关于y轴对称的分布真的是最符合神经网络训练的吗？没有任何理由能证明这点。事实上，γ和β为输出的线性调整参数，可以让分布曲线压缩或延长一点，左移或右移一点。由于γ和β是可训练的，那么意味着神经网络会随着训练过程自己挑选一个最适合的分布。如果我们固执地不用γ和β会怎么样呢？那势必会把压力转移到特征提取层，虽然最后结果依然可观，但训练压力会很大。你想想，一边只需要训练两个数，另一边需要训练特征提取层来符合最优分布就是关于y轴的对称曲线。前者自然训练成本更低。

---------------------
作者：木盏
来源：CSDN
原文：https://blog.csdn.net/leviopku/article/details/83109422
版权声明：本文为博主原创文章，转载请附上博文链接！

反向传播：https://kevinzakka.github.io/2016/09/14/batch_normalization/

在反向传播过程中，$\frac{\partial L}{\partial \boldsymbol{y}}$由上一步已经算出，是已知条件。

先求：$\frac{\partial f}{\partial \gamma }, \frac{\partial f}{\partial \hat{x_{i}}},\frac{\partial f}{\partial \beta  } $

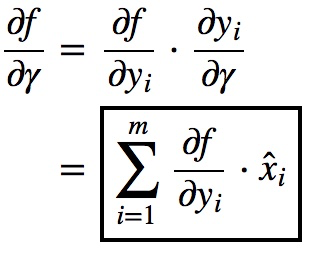
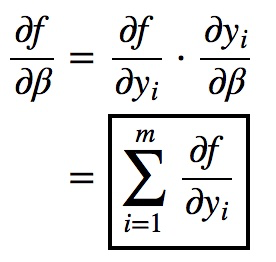
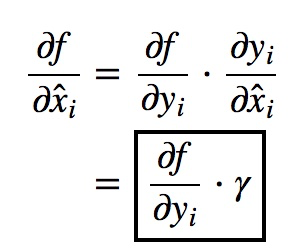
再根据 x标准化，求$\frac{\partial f}{\partial \mu }, \frac{\partial f}{\partial \sigma ^{2}},\frac{\partial f}{\partial x_{i} } $

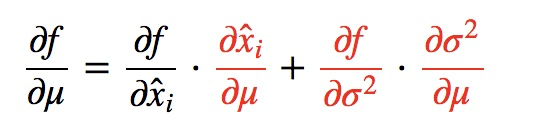
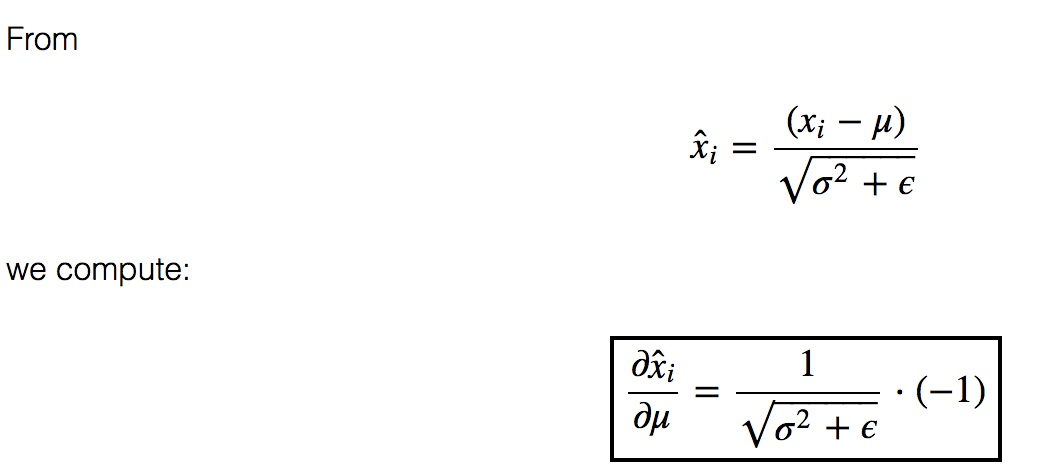
$\frac{\partial f}{\partial \mu} = \sum_{i = 1}^{m} \frac{\partial f}{\partial \hat{x}_{i}} \frac{\partial  \hat{x}_{i}}{\partial \mu} + \frac{\partial f}{\partial \sigma^{2} } \frac{\partial  \sigma^{2}}{\partial \mu}$

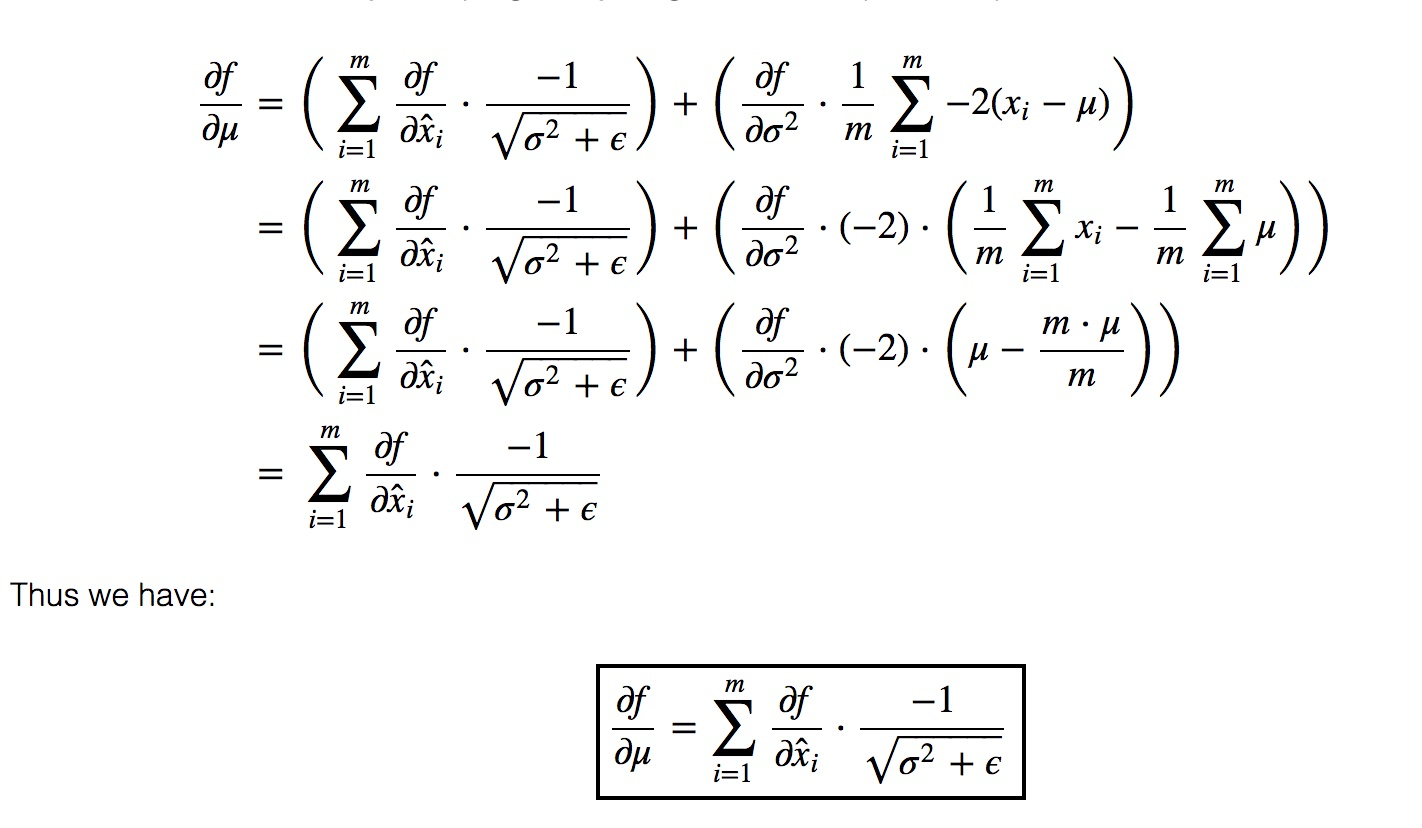
缺点：

1.对batchsize大小比较敏感，如果batchsize太不小计算的均值和方差不足以代表整体的数据分布

2.在RNN领域效果不是很好。为什么

BN是以每一个batch为基准进行计算的，也就是 μ.shape = (1, D), var.shape = (1, D),对于RNN来说，每一个batch中的数据可能不是等长的，即使padding后变成等长，然后在normalize就会引入噪声(padding)

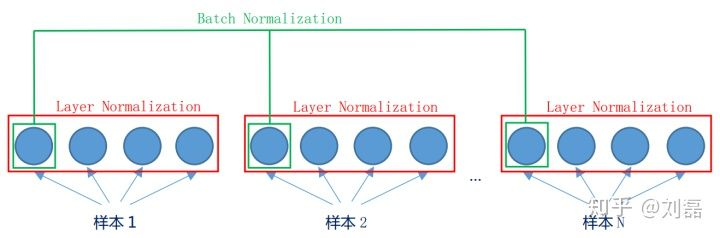
 2、Layer Normalization

LN不以batch为单位，而是以一个样本为单位。

u.shape  = (N, 1)

var.shape = (N, 1)

反向传播：

python实现：

tf接口

参考：

http://www.dataguru.cn/article-13031-1.html

https://www.cnblogs.com/guoyaohua/p/8724433.html

https://blog.csdn.net/leviopku/article/details/83109422