二分查找的变种(Java实现)

普通二分查找：

先回顾一下普通的二分查找

注意：二分查找有这样一个问题：当数组中数有重复时，比如 ｛3，3，3，3｝ 这个数组，二分查找3时，返回的是arr[1]，也就是说二分查找并不会返回3第一次出现的位置0。

public class BinarySearch {
    public static <T extends Comparable<? super T>> int search(T arr[], T value) {
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) {
            int mid = (left & right) + ((left ^ right) >> 1);
            if (arr[mid].compareTo(value) == 0) {
                return mid;
            } else if (arr[mid].compareTo(value) > 0) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        Integer[] arr = new Integer[]{1, 3, 3, 6, 7, 9};

        //-1
        System.out.println(search(arr, 0));

        //0
        System.out.println(search(arr, 1));

        //5
        System.out.println(search(arr, 9));

        //-1
        System.out.println(search(arr, 10));

        //2
        System.out.println(search(arr, 3));
    }
}　

二分变种：findFirst函数

在普通二分查找中，在[left....right]左闭右闭区间中查找，如果找到了值为value的元素就认为找到了。而在这个findFirst函数中就不是如此，在[left....right]左闭右闭区间中查找，当找到值等于value的元素后，不是让right = mid - 1，而是让right = mid，继续在[left....right]左闭右闭区间中查找。最终left== right时就退出循环。

退出循环后可能找到了value值，也有可能是循环遍历完整个数组后都没找到value，而退出循环。

所以退出循环后还要在判断一下是那种情况。

public class BinarySearch {
    public static <T extends Comparable<? super T>> int findFirst(T arr[], T value) {
        int left = 0;
        int right = arr.length - 1;
        //当left>=right时退出，这里的“=”情况与二分不同
        while (left < right) {
            int mid = (left + right) >> 1;
            if (arr[mid].compareTo(value) < 0) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        // 上面循环遍历完后。是找到了value值？还是没找到value值？判断一下。
        if (arr[left] == value) {
            return left;
        } else {
            return -1;
        }
    }

    public static void main(String[] args) {
        Integer[] arr = new Integer[]{1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 6, 7, 9};

        //-1
        System.out.println(findFirst(arr, 0));

        //0
        System.out.println(findFirst(arr, 1));

        //12
        System.out.println(findFirst(arr, 9));

        //-1
        System.out.println(findFirst(arr, 10));

        //1
        System.out.println(findFirst(arr, 3));
    }
}

二分变种：fewer函数

介绍

给定一个数组，和一个变量value,从数组中找出值最接近value值而且比value小的那个数。比如 arr = {11，22，22，33 ，33，33，44，54}   value = 33。 22最接近value，而且比value小。

所以答案是2  ( 22在数组arr中的下角标 )  。

如果没找到比value小的数，那么输出 -1。

解决思路

用二分查找方法。每次用 arr[mid] 来与value进行比对。小、等于，去左边找；大，去右边找。可能上一句的“等于”的情况你不太理解。普通二分查找是找出arr[mid] == value，而fewer函数是为了找出比value小的数，所以尽管arr[mid] == value，还得继续去左边找更小的值。

例子

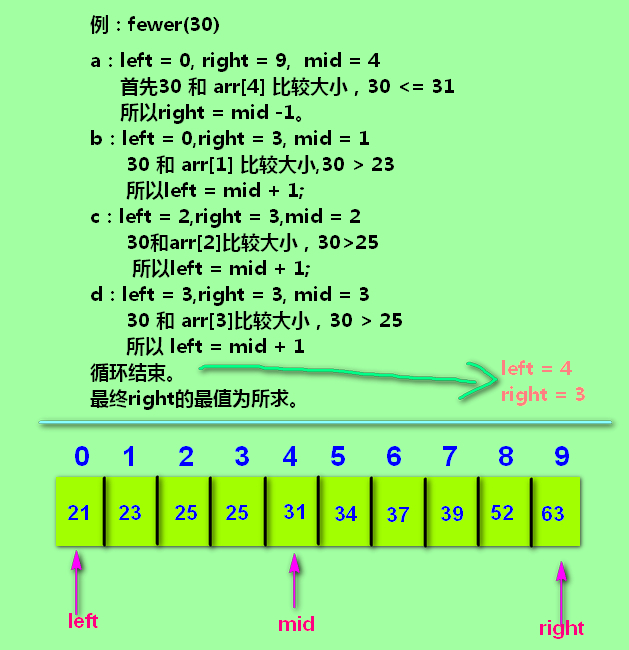
代码

public class BinarySearch {
    public static <T extends Comparable<? super T>> int fewer(T arr[], T value) {
        int left = 0;
        int right = arr.length - 1;
        //当left > right 时退出
        while (left <= right) {
            int mid = (left & right) + ((left ^ right) >> 1);
            if (value.compareTo(arr[mid]) <= 0) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return right;
    }

    public static void main(String[] args) {
        Integer[] arrF = new Integer[]{21, 23, 25, 25, 31, 34, 37, 39, 52, 63};

        //3
        System.out.println(fewer(arrF, 30));
    }
}　

二分变种：greater函数