SPOJ 422 Transposing is Even More Fun(polay计数)

题目链接：http://www.spoj.com/problems/TRANSP2/

题意：

思路：不妨设a=1,b=2,

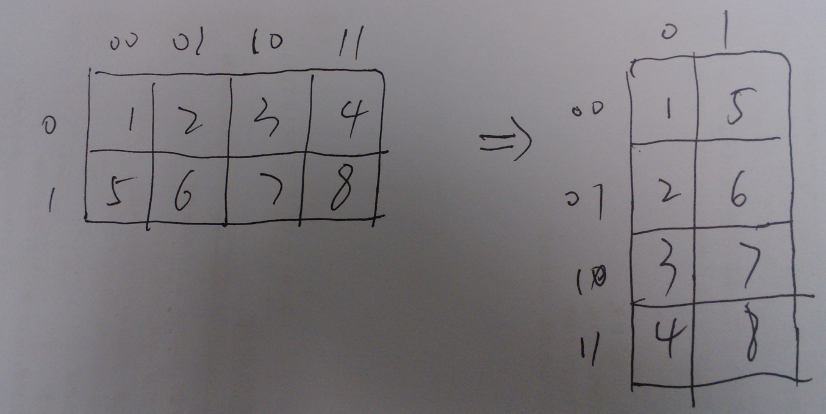
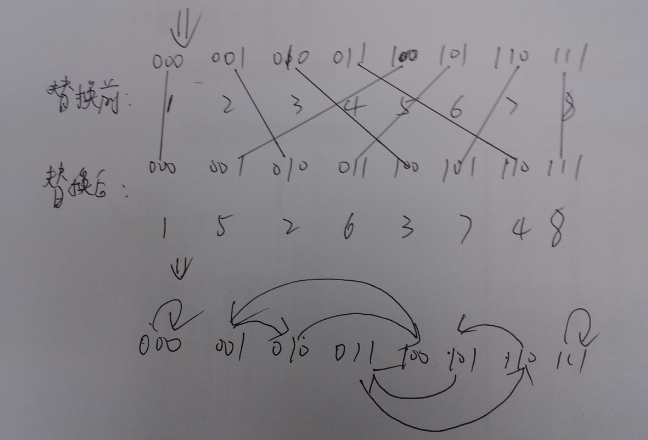
我们发现(001,010,100)组成一个置换，(011,110,101)组成一个置换。那么对于同一个置换中元素，设置换大小为x，则需要x-1次交换。因此，我们若找到循环节的个数K，那么答案即为2^(a+b)-K.

a+b个珠子的项链，每个珠子可以用两种颜色涂色，通过每次左移a个珠子得到的相同的视为相同。求不同项链的个数。问题就转化成这个。设g=Gcd(a,a+b)，则置换群个数为G=(a+b)/g。其实可以看做有G个珠子，每个珠子可以用2^g种颜色涂色。答案为：

int a,b,Pow[N],phi[N];
int prime[1005],tag[1005],cnt;

void init()
{
    Pow[0]=1;
    int i,j;
    for(i=1;i<N;i++) Pow[i]=Pow[i-1]*2%mod;

    phi[1]=1;
    for(i=2;i<N;i++) if(!phi[i]) for(j=i;j<N;j+=i)
    {
        if(!phi[j]) phi[j]=j;
        phi[j]=phi[j]/i*(i-1);
    }

    for(i=1;i<N;i++) phi[i]%=mod;

    for(i=2;i<=1000;i++) if(!tag[i])
    {
        prime[cnt++]=i;
        for(j=i+i;j<=1000;j+=i) tag[j]=1;
    }
}

int Gcd(int x,int y)
{
    if(y==0) return x;
    return Gcd(y,x%y);
}

i64 exGcd(int a,int b,i64 &x,i64 &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    i64 temp=exGcd(b,a%b,x,y);
    i64 t=x;
    x=y;
    y=t-a/b*y;
    return temp;
}

int p[105],q[105],num;

void split(int n)
{
    num=0;
    int i;
    for(i=0;i<cnt&&prime[i]*prime[i]<=n;i++) if(n%prime[i]==0)
    {
        p[num]=prime[i];
        q[num]=0;
        while(n%prime[i]==0)
        {
            q[num]++;
            n/=prime[i];
        }
        num++;
    }
    if(n>1) p[num]=n,q[num++]=1;
}

int ans,m,L;

int calPow(int a,int b)
{
    int ans=1;
    while(b)
    {
        if(b&1) ans=(i64)ans*a%mod;
        a=(i64)a*a%mod;
        b>>=1;
    }
    return ans;
}

void cal(int t)
{
    int x=L/t;
    ans+=(i64)calPow(m,t)*phi[x]%mod;
    ans%=mod;
}

void DFS(int dep,int t)
{
    if(dep==num)
    {
        cal(t);
        return;
    }
    int i;
    for(i=0;i<=q[dep];i++)
    {
        DFS(dep+1,t);
        t*=p[dep];
    }
}

int main()
{
    init();
    rush()
    {
        RD(a,b);
        if(!a||!b)
        {
            puts("0");
            continue;
        }
        b+=a;
        int k=Gcd(a,b);
        L=b/k;
        split(L); ans=0; m=Pow[k];
        DFS(0,1);
        i64 x,y;
        exGcd(L,mod,x,y);
        x=(x%mod+mod)%mod;
        ans=ans*x%mod;
        ans=Pow[b]-ans;
        ans=(ans%mod+mod)%mod;
        PR(ans);
    }
}