UNITY_MATRIX_IT_MV[Matrix]

http://blog.csdn.net/cubesky/article/details/38682975

前面发了一篇关于unity Matrix的文章。

http://blog.csdn.NET/cubesky/article/details/38664143

其中对于一般的Matrix可以说应该有一个清晰的了解了。但是对于UNITY_MATRIX_IT_MV这些matrix估计理解起来还是比较有问题。这里再重点描述一下UNITY_MATRIX_IT_MV。

首先，我们看一下unity中Doc中的描述：

UNITY_MATRIX_IT_MV

float4x4

Inverse transpose of model * view matrix.

然后我们来看一下UNITY_MATRIX_IT_MV实际的变换意义

The transpose of World2Object is the transpose of the inverse of the Object2World matrix.

• MV transforms points from object to eye space
• IT_MV rotates normals from object to eye space

And similarly:

• Object2World transforms points from object to world space
• IT_Object2World (which, as you point out, is the transpose of World2Object) rotates normals from object to world space

If it is orthogonal, the upper-left 3x3 of Object2World will be equal to that of IT_Object2World, and so will also rotate normals from object to world space.

上面这里很好的描述了UNITY_MATRIX_IT_MV的使用场景，专门针对法线进行变换。但是为什么法线的变换和定点不一样呢？让我们来看一篇推导的文章。

The gl_NormalMatrix is present in many vertex shaders. In here some light is shed on what is this matrix and what is it for. This section was inspired by the excellent book by Eric Lengyel “Mathematics for 3D Game Programming and Computer Graphics”.

Many computations are done in eye space. This has to do with the fact that lighting is commonly performed in this space, otherwise eye position dependent effects, such as specular lights would be harder to implement.

Hence we need a way to transform the normal into eye space. To transform a vertex to eye space we can write:

	vertexEyeSpace = gl_ModelViewMatrix * gl_Vertex;

So why can’t we just do the same with a normal vector? A normal is a vector of 3 floats and the modelview matrix is 4×4. Secondly, since the normal is a vector, we only want to transform its orientation. The region of the modelview matrix that contains the orientation is the top left 3×3 submatrix. So why not multiply the normal by this submatrix?

This could be easily achieved with the following code:

	normalEyeSpace = vec3(gl_ModelViewMatrix * vec4(gl_Normal,0.0));

So, gl_NormalMatrix is just a shortcut to simplify code writing or to optimize it? No, not really. The above line of code will work in some circumstances but not all.

Lets have a look at a potential problem:

;

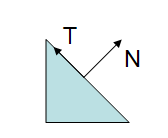
In the above figure we see a triangle, with a normal and a tangent vectors. The following figure shows what happens when the modelview matrix contains a non-uniform scale.

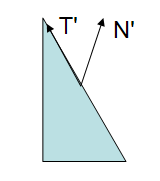
Note: if the scale was uniform, then the direction of the normal would have been preserved, The length would have been affected but this can be easily fixed with a normalization.

In the above figure the Modelview matrix was applied to all the vertices as well as to the normal and the result is clearly wrong: the transformed normal is no longer perpendicular to the surface.

We know that a vector can be expressed as the difference between two points. Considering the tangent vector, it can be computed as the difference between the two vertices of the triangle’s edge. If  and  are the vertices that define the edge we know that:

Considering that a vector can be written as a four component tuple with the last component set to zero, we can multiply both sides of the equality with the Modelview matrix

This results in

As  and  are the vertices of the transformed triangle,  remains tangent to the edge of the triangle. Hence, the Modelview preserves tangents, yet it does not preserve normals.

Considering the same approach used for vector T, we can find two points  and  such that

The main issue is that the a vector defined through the transformed points, , does not necessarily remain normal, as shown in the figures above. The normal vector is not defined as a difference between two points, as the tangent vector, it is defined as a vector which is perpendicular to a surface.

So now we know that we can’t apply the Modelview in all cases to transform the normal vector. The question is then, what matrix should we apply?

Consider a 3×3 matrix G, and lets see how this matrix could be computed to properly transform the normal vectors.

We know that, prior to the matrix transformation T.N = 0, since the vectors are by definition perpendicular. We also know that after the transformation N’.T’ must remain equal to zero, since they must remain perpendicular to each other. T can be multiplied safely by the upper left 3×3 submatrix of the modelview (T is a vector, hence the w component is zero), let’s call this submatrix M.

Let’s assume that the matrix G is the correct matrix to transform the normal vector. T. Hence the following equation:

The dot product can be transformed into a product of vectors, therefore:

Note that the transpose of the first vector must be considered since this is required to multiply the vectors. We also know that the transpose of a multiplication is the multiplication of the transposes, hence:

We started by stating that the dot product between N and T was zero, so if

then we have

Which is exactly what we want. So we can compute G based on M.

Therefore the correct matrix to transform the normal is the transpose of the inverse of the M matrix. OpenGL computes this for us in the gl_NormalMatrix.

In the beginning of this section it was stated that using the Modelview matrix would work in some cases. Whenever the 3×3 upper left submatrix of the Modelview is orthogonal we have:

This is because with an orthogonal matrix, the transpose is the same as the inverse. So what is an orthogonal matrix? An orthogonal matrix is a matrix where all columns/rows are unit length, and are mutually perpendicular. This implies that when two vectors are multiplied by such a matrix, the angle between them after transformation by an orthogonal matrix is the same as prior to that transformation. Simply put the transformation preserves the angle relation between vectors, hence transformed normals remain perpendicular to tangents! Furthermore it preserves the length of the vectors as well.

So when can we be sure that M is orthogonal? When we limit our geometric operations to rotations and translations, i.e. when in the OpenGL application we only use glRotate and glTranslate and not glScale. These operations guarantee that M is orthogonal. Note: gluLookAt also creates an orthogonal matrix!

注：之所以法线不能直接使用UNITY_MATRIX_MV进行变换，是因为法线是向量，具有方向，在进行空间变换的时候，如果发生非等比缩放，方向会发生偏移。为什么呢？拿上面的例子来说，我们可以简单的把法线和切线当成三角形的两条边，显然，三角形在空间变换的时候，不管是平移，还是旋转，或者是等比缩放，都不会变形，但是如果非等比缩放，就会发生拉伸。所以法线和切线的夹角也就会发生变化。（而切线在变换前后，方向总是正确的，所以法线方向就不正确了）。

参考：

http://www.lighthouse3d.com/tutorials/glsl-tutorial/the-normal-matrix/

http://forum.Unity3D.com/threads/_object2world-or-unity_matrix_it_mv.112446/

http://www.cnblogs.com/kesalin/archive/2012/12/06/3D_math.html