车辆运动控制算法——MPC

MPC是模型预测控制算法，在车辆运动跟踪轨迹的控制中发挥很大的优势

基础的不多说，下面记录我对LQR/MPC/二次规划问题的理解

我们从LQR来引出MPC

LQR的能量函数，目的是求函数J最小，即用最小的代价得到最好的控制效果，理论上只要系统是可控的，LQR就能求出较优的解

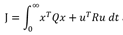
的解是 u= -K_lqr * x，这是一个线性解，用这个算法仅需要对能量函数求解一次，线下求解的u的表达式，线上不断重复计算u即可

MPC算法和LQR的公式非常接近，其表达式是离散的，函数是有边界的（算法中称之为约束条件），现实生活中，求出的解必须要对其进行限制（那车速举例，你不可能让车子跑出500km/h，这就是约束条件）

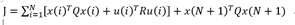
要知道，系统接下来的状态量x是根据系统当前控制量u得到的，因此需算出N+1的状态

约束条件 ：

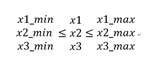
为什么会存在多组状态？

MPC的算法和LQR算法的计算量根本不是一个数量级的，因为每个时刻t=1，2，3……都需要重新求解一遍J，而MPC是根据当前状态给出接下来的控制量和状态量的序列（相比LQR仅算出一次u的表达式，MPC要计算N次，这里N指步长）

u（1），x..., u（2），x...,u（3）……u（N），然后选取第一个u（1）作为当前控制量，等到下一时刻，所有的控制量u和状态量x的序列又重新计算，再次取新的u（1）作为现在时刻的控制量，或许有人会疑问，这样不是浪费计算量么？ 我们要搞清楚，MPC的原理，他是为了接下来的预测出来的控制量控制出来的假想出的状态来判断，来给出当前最优的控制量，和大多数控制算法只关注当前时刻的状态是不同的。这也是为什么MPC是目前自动驾驶车辆运动控制算法的首选。

二次规划问题

MPC的离散公式其实就是求关于x（i）和u（i）的函数的积分，假设该函数为f（x(i),u(i)），那么二次优化就是求出函数f的优化形式，由于f的计算涉及到大量矩阵，因此所选用的优化方法主要就是减少运算次数，缩短MPC的计算时间，以达到车辆高速运动时的快速响应。

Matlab为我们提供了一个函数quadprog（），其简单调用形式为quadprog(H, f, A, b, Aeq, beq, lb, ub, x0, options)

H： 二次规划中的二次项矩阵

f： 二次规划中的一次项矩阵

Aeq： 线性不等约束的系数矩阵

beq： 线性不等约束的右端向量

lb/ub： 自变量下/上限（有些理想问题没有上下限，可不做考虑）

x0： 热启动项

（我们认为状态量不会突然变化，因此k+1时刻的最优解将会在k时刻最优解的附近，这个思路能够节约大量时间，很抱歉之前写成了初始状态，具体怎么设置我们后续更新，初学者可先设为空或0）

options:解二次规划问题的具体算法（quadprog之是提供了借口，解二次规划问题需要options指定具体算法）

客官莫急，稍后会讲怎么求得以上参数

二次规划问题基本公式：

约束条件：

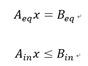
前面我们已经知道，二次规划是关于x1和x2的函数，（x = [x1; x2]）套用上面的基本公式就能得到quadprog函数的参数

现在是结合mpc的二次规划问题，目的也是求出quadprog函数的参数：

这是一个离散系统：

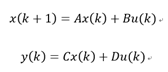
能量函数（cost function）：

我们看到了LQR的影子，但是这个P是什么呢？官方的解释终于来了，LQR的条件是状态k（此时是离散的）是趋近于无穷的，而MPC的预测步数N是有限的，为了保证系统的最终稳定性，P要尽量等于步长N到无穷时的状态，让它更贴近于LQR，但是P不可能完全等于LQR中的无穷状态，（因此我们在这写成了尽量等于），为了使MPC更像LQR，在quadprog函数加入上下边界lb和ub，P与quadprog函数的上下限一起保证了MPC稳定性。

那么P怎么求得？我们后续更新o(^▽^)o

quadprog函数的参数一般有两种求法——稀疏和稠密法，现在是稀疏法：

新的二次规划问题：

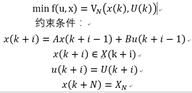
（编辑/粘贴公式真的烦）

X是x的可行域，U是u的可行域

以上公式被简化成这样：

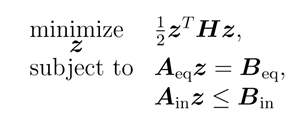
其中

事实上我们在不断更新Beq中的第一项x(k+0)(即当前的状态量)，通过反馈把从系统中读取的x(k)送到B处，不断更新的u在作用于系统，将新得到的x(k+1)再更新到Beq，系统就可以这样进行下去了

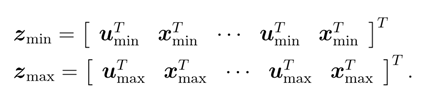
所有的Umin都是相同的，不会因时刻不同而变化，Umax也一样

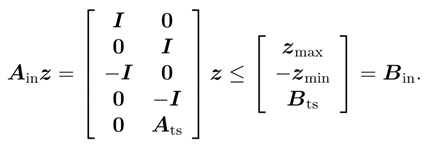
quadprog函数的lb/ub仅需要z_min和z_max，写成这样完全是因为很多算法需要这样的形式，在quadprog内部也会将z_min/z_max转换成这种形式。

MPC流程

调用quadprog函数得到的z就是控制量u和状态量x的序列，我们取第一个u作为当前控制量，等到下一时刻如法炮制出新的u。

由此可见mpc的计算量有多大

后续更新中将会讲到options参数中的优化算法

一个重要猜想：本文的矩阵设计实例依据倒摆系统，因此在Beq矩阵中，除了初始状态X(0)，其余的状态我们都希望是零，而接下来我们要加以改进应用到车辆轨迹跟踪上，因此我觉得Beq和Aeq需要调整。这个猜想后续需要验证，到时验证结果会更新在此！