poj1279.Inlay Cutters（模拟 + 枚举）

Inlay Cutters

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 2367		Accepted: 995

Description

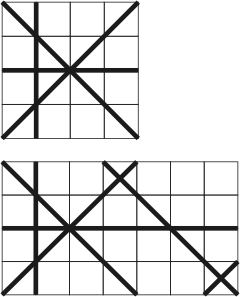The factory cuts rectangular M × N granite plates into pieces using a special machine that is able to perform cuts in 4 different directions: vertically, horizontally, and diagonally at the angle of 45 degrees to the sides of the plate. Every cut is a straight line that starts and ends on the side of the plate. 
The factory has been ordered to produce tiles for the inlay, each tile of which is a 45 degrees right triangle. To reduce the time to deliver the tiles it was decided to take all triangles from the already cut plates. Information about all performed cuts is available and your task is to compute the number of triangles of any size that were produced. 

Input

The input describes the cuts that were performed on a single rectangular plate. The first line of the input file contains three integer numbers M, N, and K, separated by spaces. M and N (1 ≤ M, N ≤ 50) are the dimensions of the plate, and K (0 ≤ K ≤ 296) is the number of cuts. Next K lines describe the cuts. ith cut is described by four integer numbers X_i,1, Y_i,1, X_i,2, and Y_i,2, separated by spaces, that represent the starting and ending point of the cut. Both starting (X_i,1, Y_i,1) and ending (X_i,2, Y_i,2) points of the cut are situated on the plate's border. Both points of the cut are different and the cut goes through the plate. Here, the coordinates by the X axis run from 0 to M, and the coordinates by the Y axis run from 0 to N. All cuts are different.

Output

Write to the output a single integer number - the number of triangles that were produced by the cuts.

Sample Input

7 4 6
6 0 7 1
1 4 1 0
0 4 4 0
0 0 4 4
0 2 7 2
7 0 3 4

Sample Output

8

Source

Northeastern Europe 2002

 #include<stdio.h>
 #include<string.h>
 #include<queue>
 using namespace std;
 int a[ * ][ * ] ;
 bool map[ * ][ * ] ;
 int col , row , cut ;
 int x1 , y1 , x2 , y2 ;
 int sum =  ;
 int move[][] = {{-,,,},{-,,,},{,,,},{,,,-},{,,,-},{,-,-,-},{,-,-,},{-,-,-,}};

 void hua1 ()
 {
     for (int i = y1 ; i <= y2 ; i++) {
         a[x1][i] +=  ;
     }
 }

 void hua2 ()
 {
     for (int i = x1 ; i <= x2 ; i++) {
         a[i][y1] +=  ;
     }
 }

 void hua3 ()
 {
     int cnt = y2 - y1 +  ;
     int x = x1 , y = y1 ;
     while (cnt--) {
         a[x][y] +=  ;
         x ++ , y ++ ;
     }
 }

 void hua4 ()
 {
     int cnt = x2 - x1 +  ;
     int x = x1 , y = y1 ;
     while (cnt--) {
         a[x][y] +=  ;
         x ++ , y-- ;
     }
 }

 bool judge1 (int x1 ,int  y1 ,int  x2 ,int y2)
 {
     int cnt = x2 - x1 -  ;
     int x = x1 +  , y = y1 +  ;
     while (cnt --) {
         if (a[x][y] !=   ) {
             return false ;
         }
         x ++ , y ++ ;
     }
     return true ;
 }

 bool judge2 (int x1 , int y1 , int x2 , int y2)
 {
     int cnt = x2 - x1 -  ;
     int x = x1 +  , y = y1 -  ;
     while (cnt--) {
         if (a[x][y] != ) {
             return false ;
         }
         x++ , y-- ;
     }
     return true ;
 }

 bool judge3 (int x1 , int y1 , int x2 , int y2)
 {
     int cnt = x2 - x1 -  ;
     int x = x1 +  ;
     while (cnt--) {
         if (a[x][y1] !=  ) {
             return false ;
         }
         x ++ ;
     }
     return true ;
 }

 bool judge4 (int x1 , int y1 , int x2 , int y2)
 {
     int cnt = y2 - y1 -  ;
     int y = y1 +  ;
     while (cnt --) {
         if (a[x1][y] != ) {
             return false ;
         }
         y ++ ;
     }
     return true ;
 }

 void bfs (int sx , int sy)
 {
    // printf ("sx = %d , sy = %d\n" , sx , sy) ;
     for (int i =  ; i <  ; i++) {
             int x1 = sx + move[i][] , y1 = sy + move[i][] ;
             int x2 = sx + move[i][] , y2 = sy + move[i][] ;
             if (x1 <  || y1 <  || x1 > row || y1 > col ) {
                 continue ;
             }
             if (x2 <  || y2 <  || x2 > row || y2 > col ) {
                 continue ;
             }
             if (a[x1][y1] * a[x2][y2] ==  ) {
                 continue ;
             }
             while(a[x1][y1] * a[x2][y2] ==  ) {
                 x1 += move[i][] ;
                 y1 += move[i][] ;
                 x2 += move[i][] ;
                 y2 += move[i][] ;
             }
             if (a[x1][y1] * a[x2][y2] ==  ) {
                 continue ;
             }
             if (a[x1][y1] ==  || a[x2][y2] == ) {
                 continue ;
             }
             if (x1 != x2) {
                 int k = (y2 - y1) / (x2 - x1) ;
                 if (k == ) {
                     if (x1 > x2) {
                         x1 ^= x2 ^= x1 ^= x2 ;
                         y1 ^= y2 ^= y1 ^= y2 ;
                     }
                     if (judge1 (x1 , y1 , x2 , y2) ) {
                         sum ++ ;
                     }
                 }
                 else if (k == -) {
                     if (x1 > x2) {
                         x1 ^= x2 ^= x1 ^= x2 ;
                         y1 ^= y2 ^= y1 ^= y2 ;
                     }
                     if ( judge2 (x1 , y1 , x2 , y2) ) {
                         sum ++ ;
                     }
                 }
                 else {
                     if (x1 > x2) {
                         x1 ^= x2 ^= x1 ^= x2 ;
                     }
                     if ( judge3 (x1 , y1 , x2 , y2) ) {
                         sum ++ ;
                     }
                 }
             }
             else {
                 if (y1 > y2) {
                     y1 ^= y2 ^= y1 ^= y2 ;
                 }
                 if ( judge4 (x1 , y1 , x2 , y2) ) {
                     sum ++ ;
                 }
             }
         }
 }

 int main ()
 {
     // freopen ("a.txt" , "r" , stdin ) ;
     scanf ("%d%d%d" , &col , &row , &cut ) ;
     col *=  , row *=  ;
     for (int i =  ; i <= row ; i++) {
         a[i][col] +=  ;
         a[i][] +=  ;
     }
     for (int i =  ; i <= col ; i++) {
         a[row][i] +=  ;
         a[][i] +=  ;
     }
     while (cut--) {
         scanf ("%d%d%d%d" , &y1 , &x1 , &y2 , &x2 ) ;
         x1 *=  , y1 *=  , x2 *=  , y2 *=  ;
         if (x1 == x2) {
             if (y1 > y2) {
                 y1 ^= y2 ^= y1^= y2 ;
             }
             hua1 () ;
         }
         else if (y1 == y2) {
             if (x1 > x2) {
                 x1 ^= x2 ^= x1 ^= x2 ;
             }
             hua2 () ;
         }
         else if ( (y2 - y1) / (x2 - x1) == ) {
             if (y1 > y2) {
                 y1 ^= y2 ^= y1^= y2 ;
                 x1 ^= x2 ^= x1 ^= x2 ;
             }
             hua3 () ;
         }
         else if ( (y2 - y1) / (x2 - x1) == - ) {
             if (x1 > x2) {
                 y1 ^= y2 ^= y1^= y2 ;
                 x1 ^= x2 ^= x1 ^= x2 ;
             }
             hua4 () ;
         }
     }

    /* for (int i = 0 ; i <= row ; i++) {
         for (int j = 0 ; j<= col ; j++) {
             printf ("%d " , a[i][j]) ;
         }
         puts ("") ;
     }*/

     for (int i =  ; i <= row ; i++) {
         for (int j =  ; j <= col ; j++) {
             if (a[i][j] > ) {
                 bfs (i , j) ;
             }
         }
     }
     printf ("%d\n" , sum ) ;

 }