最短路径——Dijkstra（简易版）

简易之处：顶点无序号，只能默认手动输入0，1，2...（没有灵活性）

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <malloc.h>

using namespace std;

const int VERTEX_NUM = 20;
const int INFINITY = 0x3fffffff;

bool vis[VERTEX_NUM];
int dist[VERTEX_NUM];					// 源点到各点的距离
int pre[VERTEX_NUM];

class Graph {
public:
	int vexNum;
	int edgeNum;
//	int vex[VERTEX_NUM];
	int arc[VERTEX_NUM][VERTEX_NUM];
};

void createGraph(Graph &G)
{
	int i, j, w;
	cout << "请输入无向图的顶点数和边数：";
	cin >> G.vexNum >> G.edgeNum;				// 默认顶点序号为0 1 2 3...
	for (int i = 0; i != G.vexNum; ++i) {
		for (int j = 0; j != G.vexNum; ++j) {
			G.arc[i][j] = INFINITY;
		}
	}
	for (int k = 0; k != G.edgeNum; ++k) {
		cout << "请输入边(vi, vj)的顶点i、j以及该边的权w：";
		cin >> i >> j >> w;
		G.arc[i][j] = w;
		G.arc[j][i] = w;
	}
}

// Dijkstra算法
void Dijkstra(Graph &G, int src)
{
	memset(vis, false, VERTEX_NUM);
	memset(dist, INFINITY, VERTEX_NUM);
	vis[src] = true;
	for (int i = 0; i != G.vexNum; ++i) {
		dist[i] = G.arc[i][src];
		pre[i] = src;
	}
	int lowcost = INFINITY;
	int lowcostIndex = src;
	for (int cnt = 1; cnt != G.vexNum; ++cnt) {
		lowcost = INFINITY;
		for (int i = 0; i != G.vexNum; ++i) {
			if (dist[i] < lowcost && !vis[i]) {
				lowcost = dist[i];
				lowcostIndex = i;
			}
		}
		vis[lowcostIndex] = true;
		for (int i = 0; i != G.vexNum; ++i) {
			if (!vis[i] && G.arc[lowcostIndex][i] != INFINITY && lowcost + G.arc[lowcostIndex][i] < dist[i]) {
				dist[i] = G.arc[lowcostIndex][i] + lowcost;
				pre[i] = lowcostIndex;
			}
		}
	}
}

int main()
{
	Graph G;
	createGraph(G);
	cout << "请输入源点：";
	int source;
	cin >> source;
	Dijkstra(G, source);
	for (int i = 0; i != G.vexNum; ++i) {
		if (i == source)	continue;
		cout << "源点" << source << "到点" << i << "的距离为" << dist[i] << endl;
	}

	return 0;
}

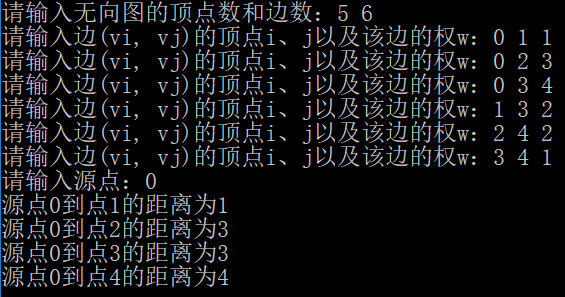
测试方法及结果：