ckfinder 1
网上的破解教程对于2.4版本来说已经过时了。
以下是CKFinder 2.4 ASP.NET的亲测可用破解方法,经测试,只需修改两处代码。
打开ckfinder.js,
- 步骤1. 搜索替换如下代码:

var r = "\074\x64\x69\x76\040\143\x6c\x61\x73\163\x3d\047\x76\x69\x65\x77\x20\x74\x6f\157\x6c\x5f\x70\x61\x6e\145\x6c\047\040\x73\x74\x79\x6c\145\075\047\x70\141\144\144\x69\156\x67\072\x32\160\x78\x3b\x64\x69\163\x70\x6c\x61\x79\x3a\142\154\x6f\143\x6b\040\041\x69\x6d\160\x6f\162\x74\141\156\x74\x3b\160\157\163\x69\164\x69\157\156\072\163\x74\x61\x74\x69\143\x20\x21\151\x6d\160\157\x72\164\x61\156\x74\x3b\x63\157\x6c\x6f\x72\x3a\x62\154\x61\x63\153\x20\041\151\155\x70\x6f\x72\164\x61\156\164\x3b\142\141\x63\153\147\162\157\165\x6e\144\055\143\x6f\x6c\157\x72\072\x77\150\151\x74\x65\040\041\151\155\160\x6f\162\x74\141\156\x74\x3b\x27\076",s="\074\057\x64\151\x76\076",t=r+"\124\x68\151\x73\x20\x69\x73\x20\x74\150\x65\040\104\x45\x4d\x4f\x20\x76\x65\x72\163\151\x6f\x6e\x20\x6f\146\040\x43\x4b\106\151\156\x64\x65\162\056\x20\x50\154\145\x61\163\x65\x20\166\151\163\x69\164\040\164\150\x65\040\074\141\x20\150\162\145\146\x3d\047\x68\164\164\160\x3a\x2f\x2f\x63\153\x73\157\x75\x72\x63\x65\x2e\x63\x6f\x6d\057\143\153\x66\x69\x6e\x64\145\x72\x27\x20\x74\141\162\x67\145\x74\075\x27\137\142\x6c\x61\156\153\x27\076\x43\x4b\x46\151\156\144\x65\162\040\167\145\142\x20\163\151\164\145\074\057\141\x3e\040\x74\x6f\040\157\142\164\141\151\156\040\141\x20\x76\141\154\x69\x64\040\154\151\143\x65\x6e\x73\x65\x2e"+s,u=r+"\103\x4b\x46\x69\x6e\144\145\162\040\104\x65\x76\145\154\157\160\x65\162\x20\114\x69\143\x65\156\163\x65\x3c\142\162\x2f\x3e\114\151\143\145\x6e\x73\x65\144\040\x74\x6f\072\x20";

替换为:
|
1
|
var r = "\x20",s="\x20",t="\x20",u="\x20"; |
这是删除树形菜单下方的广告提示,删除后便不会再出现广告。
- 步骤2. 搜索替换如下代码:
|
1
|
if((V.eu&& !aa||Z)&&V.mj) |
替换后:
|
1
|
if((V.eu&& !aa||Z)&&V.mj&&V.mj!=O) |
这是针对图片列表上方的广告提示,O就是存放广告代码的变量。
修改后的效果图:
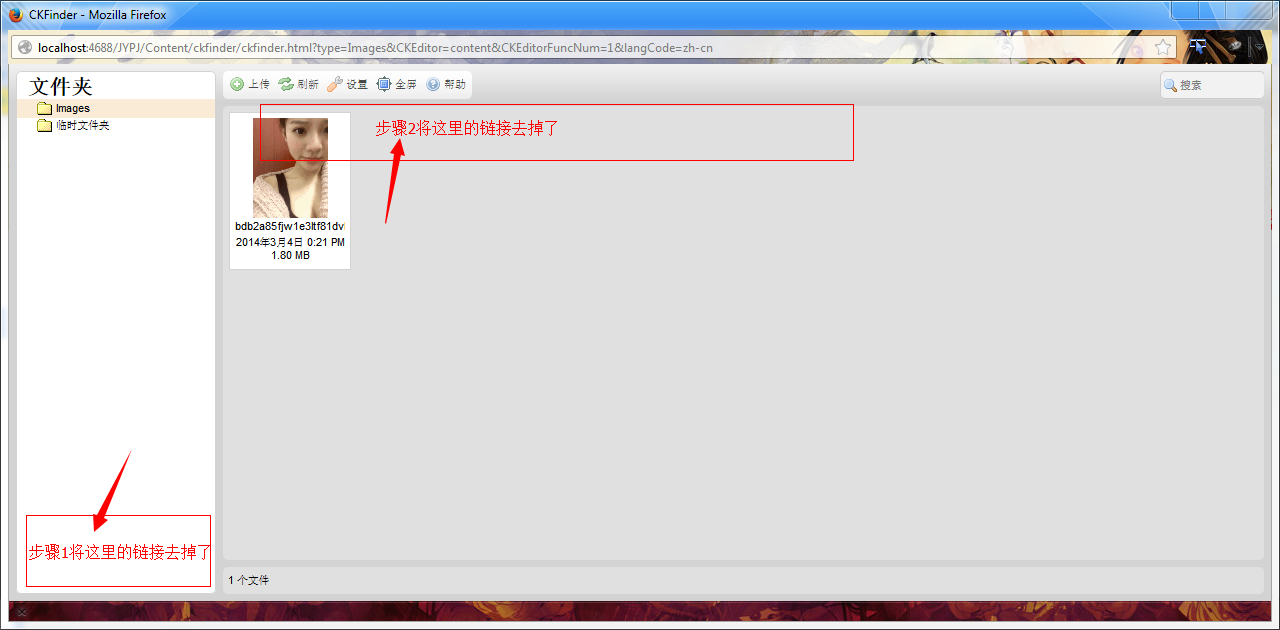
ckfinder 1的更多相关文章
- MVC配置ckeditor+ckfinder
ckeditor当前使用版本:4.5.8 ckfinder当前使用版本:2.6.0 1.Ckeditor配置简单,直接使用Nuget下载就可 2.下载ckfinder https://cksource ...
- CKEditor与CKFinder整合 MVC3
今天偶然看到一篇关于 CKEditor与CKFinder整合文章,心想有一段时间没有使用这种东西了.于是乎自己动手亲自体验了一下,本以为简单但在东西编写的过程发现了很多没有遇见毛病. 所以记录一下自己 ...
- 基于MVC4+EasyUI的Web开发框架经验总结(5)--使用HTML编辑控件CKEditor和CKFinder
Web开发上有很多HTML的编辑控件,如CKEditor.kindeditor等等,很多都做的很好,本文主要介绍在MVC界面里面,CKEditor的配置和使用.CKEditor的前身是FCKEdito ...
- CKEditor与CKFinder的配置(ASP.NET环境)
CKEditor是一个专门使用在网页上的所得文字编辑器,适用于PHP.ASP.NET.Java等后端开发语言.CKEditor原名为FCKeditor,“FCK” 是这个编辑器的作者的名字Freder ...
- 单独使用CKfinder上传图片
首先引入ckfinder.js <script type="text/javascript" src="<%=request.getContextPath() ...
- .net环境下ckeditor与ckfinder中文文件链接乱码的问题
.net环境下ckeditor与ckfinder中文文件链接乱码的问题 将ckfinder.js中的getUrl:function(){return this.folder.getUrl()+enco ...
- .net_ckeditor+ckfinder的图片上传配置
CKEditor和CKFinder的最新版可以到官方网站(http://cksource.com)上下载获得. 把以上两个资源放到网站的根目录: /CKEditor 和 /CKFinder (不区分大 ...
- struts2整合CKEditor和CKFinder实现上传
上一篇文章给大家分享了CKEditor+CKFinder+JSP实现了在线编辑器上传图片的功能,这里在给大家分享一下如何在前面的基础上在struts2下实现这样的功能. 实现与Struts2的整合,整 ...
- jsp中如何整合CKEditor+CKFinder实现文件上传
最近笔者做了一个新闻发布平台,放弃了之前的FCKEditor编辑器,使用了CKEditor+CKFinder,虽然免费的CKFinder是Demo版本,但是功能完整,而且用户都是比较集中精神发新闻的人 ...
- ASP.NET版CKEditor与CKFinder的配置使用
ASP.NET版 CKEditor与CKFinder的配置使用 将CKEditor 与 CKFinder 的包含在项目中,并添加程序集的引用 从http://cksource.com网站上下载CKEd ...
随机推荐
- SVN版本控制图标不显示的解决方法~
新系统每次装了svn之后,过了一段时间,安装的软件一多就会出现这个问题,哎,收录一下解决方案! 输入:win+R,输入regedit,调出注册表信息,按下Ctrl+F,在注册表里搜索"She ...
- 用arm-linux-gcc v4.3.4交叉编译Qt4.8.3
1.解压缩 #tar zxvf qt-everywhere-opensource-src-4.8.3.tar.gz 2. configure #mkdir buildarm-static #cd b ...
- JavaScript 获取当月天数
getDate() 方法可返回月份的某一天.取值范围是1~31 如果是0的话,就返回最后一天.这样就能取得当月的天数了 比如获取16年2月份的天数 var day = new Date(2016,2, ...
- pkg-config相关的常用指令
pkg-config用途: 查询系统已安装库的基础信息(元信息) 1.查看所有的pkg-config库 pkg-config --list-all --list-all 列出pkg-config路径 ...
- Day12 线程池、RabbitMQ和SQLAlchemy
1.with实现上下文管理 #!/usr/bin/env python# -*- coding: utf-8 -*-# Author: wanghuafeng #with实现上下文管理import c ...
- Python Tutorial 学习(十)-- Brief Tour of the Standard Library
10.1. Operating System Interface os库 import os os.getcwd() # Return the current working directory 'C ...
- 离散傅里叶变换(DFT)
目录 一.研究的意义 二.DFT的定义 三.DFT与傅里叶变换和Z变换的关系 四.DFT的周期性 五.matlab实验 五.1 程序 ...
- ESXI转HYPER-V,问题接二连三啊(VMDK转VHD)
首先说软件: 要不是用SCVMM来转的话,我用得最爽的还是WINIMAGE,自然流畅.其它的都有各种问题. 其次说说配置更改: 如果原ESXI里只有一个硬盘,一切好说,如果里面挂载了两个,甚至三个硬盘 ...
- h.264直接预测
直接预测是B帧上一种独有的预测方式,其中直接预测又分为两种模式: 时域直接模式(temporal direct).空域直接模式(spatial direct). 在分析这两种模式之前,有一个前提概念需 ...
- 转:阿里旺旺导致python安装包失败的解决办法
我以前使用web.py没事,今天运行时报错, mimetypes.init() # try to read system mime.types File "D:\ProgramFiles\p ...
