Unity学习(十三)场景优化之四叉树

http://blog.sina.com.cn/s/blog_89d90b7c0102wyfw.html

四叉树是在二维图片中定位像素的唯一适合的算法。因为二维空间（图经常被描述的方式）中，平面像素可以重复的被分为四部分，树的深度由图片、计算机内存和图形的复杂度决定。

四叉树（quad-tree）是一种数据结构，是一种每个节点最多有四个子树的数据结构。四叉树可以用来在数据库中放置和定位文件（称作记录或键）。这一算法通过不停的把要查找的记录分成4部分来进行匹配查找直到仅剩下一条记录为止。在树中，记录被存储在叶子的位置上。这一名字的由来是因为记录被存储在端点上，它们上面再没有节点了。分支被称作节点。数的顺序是每节点的分支（也称孩子）数。在四叉树中，每个节点通常有4个孩子，因此顺序是4。四叉树的叶子数也是4。为达到想要的记录所进行的查找操作次数成为树的深度。

        四叉树在游戏场景中的应用非常普遍，比如大场景的物件动态加载，NPC动态加载等，只用显示玩家周围的对象，能非常有效的降低场景CPU和GPU消耗。

四叉树的查找算法，通过遍历子节点只到找到与之相交的叶子节点，就不做记录了，在这里将玩家移动时，周围物件显示和隐藏的过程记录下来，以便日后能快速回忆。
主角刚进入游戏场景时
（蓝色表示【玩家所在叶子节点】，绿色表示【进入列表】，白色表示【显示列表】）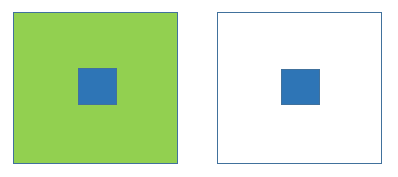
焦点不动时

1.没有【当前显示列表】，那么焦点周围的点都为【进入列表】

2.【进入列表】中的叶子节点执行swapIn方法加入【进入队列】

刷新队列

3.如果叶子节点都执行过swapIn，并且可见，就加入到当前【当前显示列表】，并从【进入队列】中移除
主角移动时
（绿色表示【进入列表】，红色表示【出去列表】）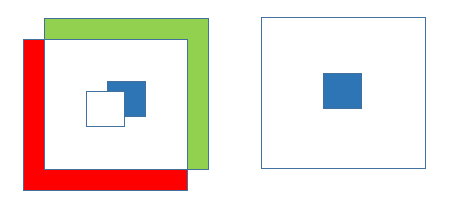
当焦点移动时

1.通过【当前显示列表】和【距离】筛选出此时的【进入列表】和【出去列表】

2.【进入列表】中的叶子节点执行swapIn方法加入【进入队列】

3.【出去列表】中的叶子节点执行swapOut方法加入【出去队列】

刷新队列

4.如果叶子节点都执行过swapIn，并且可见，就加入到当前【当前显示列表】，并从【进入队列】中移除

5.如果叶子节点都执行过swapOut，并且不可见，就从【出去队列】中移除

学习参考：

http://www.unity.5helpyou.com/3416.html