某关于数位DP的一节课后的感受

题目

求给定区间[x,y]中满足下列条件的整数个数，这个数恰好等于k个互不相等的B的整数次幂之和

Input

15 20 2 2

Out

17 18 20

示例：17=2⁴+2⁰ 18=2⁴+2¹ 20=2⁴+2²

为什么15和16不行呢？？？ 因为15=2³+2²+2¹+2⁰ 此时K>2明显不成立 而16=2³+2³

此时B明显相等就无法通过 其实我们可以把它当成B进制的数来算（~~其实我也是听老师讲的~~）

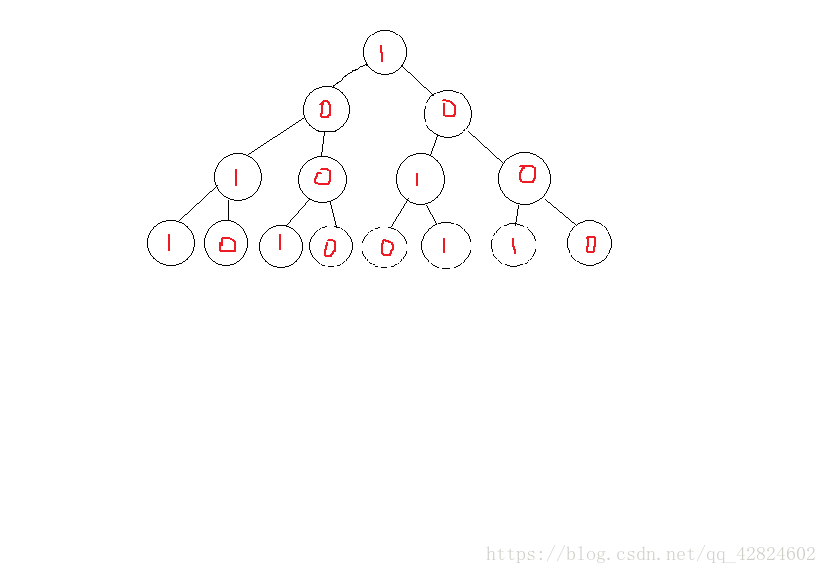
在这里我们把它化成一棵树 然后转化成0，1的格式，去寻找它的一的数量是否符合所要求的数

Such As

（好丑，其实是闲着蛋疼画的【图不一定是对的只是为了看得明显一点......】）

这样就可以在树里寻找所满足条件的结果 为什么用0和1呢

Because Of

17=2^4+2^0

18=2^4+2^1

20=2^4+2^2

这个实际上就是B进制数

如下：

17=1*2^4+0*2^3+0*2^2+1*2^1+0*2^0

17=10001

同理18=10010 20=10100 15=1111 16=10000

所以说可以在树中找它的1的数量就可以找出答案

//对f进行预处理（变得多多的。。。）
void init(){
    f[][]=;
    for(int i=;i<=;i++){
        f[i][]=f[i-][];
        for(int j=;j<=i;j++)
            f[i][j]=f[i-][j]+f[i-][j-];//状态转移方程
    }
}

为了给它放进树里所做的努力！！！

然后去搜寻树中的1，一般情况下左子树的1要比右子树的一来得少

当满足条件时就可以记录下来

上面的例子中可以看出有两个1即可

此时就可以存储。。。

int cal(int x,int k){
    int tot,ans;//tot当前路径还有的1的个数
    for(int i=;i>;i--){
        if(x&(<<i)){
            tot++;
            if(tot>k)break;
            x=x^(<<i);
        }
        if(<<(i-)<=x){
        ans+=f[i-][k-tot];
        }
    }
    if((tot+x)==k) ans++;
    return x;
}

答案的输出

cal(y,k)-cal(x-,k) 

这个答案的取值

嗯......

用上面做示范：

就是：

[1,20]--[1,14]=[15,20]

基本没错啦

（这个[x,y]是区间的意思）

这样可以找到答案

（如果有错敬请各位大佬指出）

跪地求RP