最短路径——Floyd-Warshall算法

Floyd-Warshall算法，简称Floyd算法，用于求解任意两点间的最短距离，时间复杂度为O(n^3)。

我们平时所见的Floyd算法的一般形式如下：

 void Floyd()
 {
      int i,j,k;
      for(k=;k<=n;k++)
          for(i=;i<=n;i++)
              for(j=;j<=n;j++)
                  if(dist[i][k]+dist[k][j]<dist[i][j])
                      dist[i][j]=dist[i][k]+dist[k][j];
 ｝

注意下第6行这个地方，如果dist[i][k]或者dist[k][j]不存在，程序中用一个很大的数代替。最好写成if(dist[i][k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]<dist[i][j])，从而防止溢出所造成的错误。
  上面这个形式的算法其实是Floyd算法的精简版，而真正的Floyd算法是一种基于DP(Dynamic Programming)的最短路径算法。

例题分析：

设图G中n 个顶点的编号为1到n。令c [i, j, k]表示从i 到j 的最短路径的长度，其中k 表示该路径中的最大顶点，也就是说c[i,j,k]这条最短路径所通过的中间顶点最大不超过k。因此，如果G中包含边<i, j>，则c[i, j, 0] =边<i, j> 的长度；若i= j ，则c[i,j,0]=0；如果G中不包含边<i, j>，则c (i, j, 0)= +∞。c[i, j, n] 则是从i 到j 的最短路径的长度。   对于任意的k>0，通过分析可以得到：中间顶点不超过k 的i 到j 的最短路径有两种可能：该路径含或不含中间顶点k。若不含，则该路径长度应为c[i, j, k-1]，否则长度为 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取两者中的最小值。   状态转移方程：c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]}，k＞0。   这样，问题便具有了最优子结构性质，可以用动态规划方法来求解。

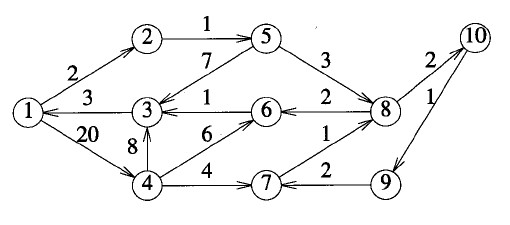
为了进一步理解，观察上面这个有向图：若k=0, 1, 2, 3，则c[1,3,k]= +∞；c[1,3,4]= 28；若k = 5, 6, 7，则c [1,3,k] = 10；若k=8, 9, 10，则c[1,3,k] = 9。因此1到3的最短路径长度为9。   下面通过程序来分析这一DP过程，对应上面给出的有向图：

 #include <iostream>
 using namespace std;

 const int INF = ;
 int n=,map[][],dist[][][];
 void init()
 {
     int i,j;
     for(i=;i<=n;i++)
         for(j=;j<=n;j++)
             map[i][j]=(i==j)?:INF;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
 }
 void floyd_dp()
 {
     int i,j,k;
     for(i=;i<=n;i++)
         for(j=;j<=n;j++)
             dist[i][j][]=map[i][j];
     for(k=;k<=n;k++)
         for(i=;i<=n;i++)
             for(j=;j<=n;j++){
                 dist[i][j][k]=dist[i][j][k-];
                 if(dist[i][k][k-]+dist[k][j][k-]<dist[i][j][k])
                     dist[i][j][k]=dist[i][k][k-]+dist[k][j][k-];
             }
 }
 int main()
 {
     int k,u,v;
     init();
     floyd_dp();
     while(cin>>u>>v,u||v)
     {
         for(k=;k<=n;k++)
         {
             if(dist[u][v][k]==INF) cout<<"+∞"<<endl;
              else cout<<dist[u][v][k]<<endl;
         }
     }
     return ;
  }

Floyd-Warshall算法不仅能求出任意2点间的最短路径，还可以保存最短路径上经过的节点。下面用精简版的Floyd算法实现这一过程，程序中的图依然对应上面的有向图。

 #include <iostream>
  using namespace std;

  const int INF = ;
  int n=,path[][],dist[][],map[][];
  void init(){
      int i,j;
      for(i=;i<=n;i++)
          for(j=;j<=n;j++)
             map[i][j]=(i==j)?:INF;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
     map[][]=,map[][]=,map[][]=;
 }
 void floyd(){
     int i,j,k;
     for(i=;i<=n;i++)
         for(j=;j<=n;j++)
             dist[i][j]=map[i][j],path[i][j]=;
     for(k=;k<=n;k++)
         for(i=;i<=n;i++)
             for(j=;j<=n;j++)
                 if(dist[i][k]+dist[k][j]<dist[i][j])
                     dist[i][j]=dist[i][k]+dist[k][j],path[i][j]=k;
 }
 void output(int i,int j){
     if(i==j) return;
     if(path[i][j]==) cout<<j<<' ';
     else{
         output(i,path[i][j]);
         output(path[i][j],j);
     }
 }
 int main(){
     int u,v;
     init();
     floyd();
     while(cin>>u>>v,u||v){
         if(dist[u][v]==INF) cout<<"No path"<<endl;
         else{
             cout<<u<<' ';
             output(u,v);
             cout<<endl;
         }
     }
     return ;
 }

输入 1 3                    
  输出 1 2 5 8 6 3

转自：Floyd-Warshall算法DP流程详解