RB-Tree深度探索

关联式容器就是通过key值来寻找value，这个和数据库很相像，为了提升查找效率，因此关联式容器底层大多数用红黑树或哈希表来实现。

红黑树是高度平衡的二叉树，它也被称为平衡二元搜索树。

如上所示，正常++ite的访问出来的顺序即为中序遍历：5,6,7,8,10,11,12,13,15

set有两种插入方式，insert_unique()和insert_equal()，insert_unique即为插入的元素不允许重复，insert_equal()为插入的元素可以相同。

尝试定义一个红黑树，其类模板的第一个参数是key的type，第二个参数为value的type（当key与value类型相同即表明无key与value之分，key即为value），value由key和data合成，第三个参数是告诉类模板如何从value中取出key（下图用来STL模板库中的identity类来返回这个值本身，identity对()操作符进行了重载，自身并没有数据成员，所以这个类的实例化的对象其行为像一个函数，所以我们称它为仿函数、或函数对象。ps：identity是gun c独有的，并非所有STL模板库都含有），第四个参数是比较方式（下图中的less和前一个identity类似），第五个参数为空间配置器，默认使用alloc。

测试程序

#include<iostream>
#include <set>
#include <functional>
using namespace std;
void test_Rb_tree()
{
	cout << "\ntest_Rb_tree().......... \n";

	_Rb_tree<int, int, _Identity<int>, less<int>> itree;
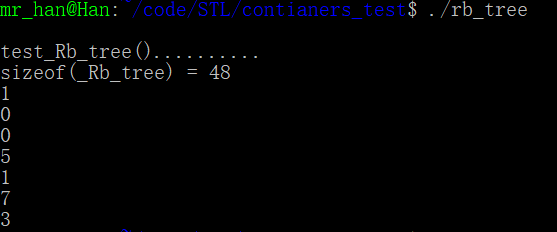
	cout<<"sizeof(_Rb_tree) = "<<sizeof(_Rb_tree<int, int, _Identity<int>, less<int>>)<<endl;//这里大小可能不是12或24，具体和自己的STL库版本有关
	cout << itree.empty() << endl;  //1
	cout << itree.size() << endl;   //0

	itree._M_insert_unique(3);
	itree._M_insert_unique(8);
	itree._M_insert_unique(5);
	itree._M_insert_unique(9);
	itree._M_insert_unique(13);
	itree._M_insert_unique(5);  //no effect, since using insert_unique().
	cout << itree.empty() << endl;  //0
	cout << itree.size() << endl;   //5
	cout << itree.count(5) << endl; //1

	itree._M_insert_equal(5);
	itree._M_insert_equal(5);
	cout << itree.size() << endl;   //7, since using insert_equal().
	cout << itree.count(5) << endl; //3
}
int main()
{
	test_Rb_tree();
	return 0;
}

运行一下