强化学习实战 | 表格型Q-Learning玩井字棋（二）

在 强化学习实战 | 表格型Q-Learning玩井字棋（一）中，我们构建了以Game() 和 Agent() 类为基础的框架，本篇我们要让agent不断对弈，维护Q表格，提升棋力。那么我们先来盘算一下这几个问题：

• Q1：作为陪练的一方，策略上有什么要求吗？
• A1：有，出棋所导致的状态要完全覆盖所有可能状态。满足此条件下，陪练的棋力越强（等同于环境越严苛），agent训练的效果越好。AlphaGo的例子告诉我们，陪练的策略也是可以分阶段调整的：前期先用人类落子的预测模型当陪练，中后期让agent自我博弈。在井字棋的例子中，环境较简单，可以直接让agent自我博弈，采用 ε-greedy 策略（贪心地选择Q值最大的动作执行，并以 ε 的概率试探其他的动作）即可实现可能状态的覆盖。
• Q2：采用自我博弈的方式，也就意味着，在陪练动作前，也要调用Q表格，是吗？
• A2：是，不仅是调用，如果当前状态不在Q表格中，还要往Q表格中新增状态，否则无法将执行 ε-greedy 策略。
• Q3：而且陪练动作之后，还要更新Q表格？
• A3：是。
• Q4：环境的定义是以一方的视角分配奖励的，对于陪练来说，不能简单地调用Q表格进行决策吧？假设agent是蓝方，陪练是红方，直接用Q表进行决策，那么红方就是以自身落蓝字进行考虑的，所考虑的状态完全是非法的——例如场上仅有一个蓝子，此刻又是待落蓝子。
• A4：对，不能简单调用！在陪练动作前，要把视角翻转——如果当前状态是 [1, -1, 0, 0, 0, 0, 0, 0, 1]，翻转就是把当前状态视作 [-1, 1, 0, 0, 0, 0, 0, 0, -1]，再考虑自身如何落蓝子。

再回想一下Q-Learning算法：

细节也就逐渐清晰了，我们要实现的目标如下：

1. 维护记录蓝方上一状态，动作及奖励的变量组 lastState_blue，lastAction_blue，lastReward_blue；维护记录红方上一状态，动作及奖励的变量组 lastState_red，lastAction_red，lastReward_red。（要时刻注意，一方行动之后的状态并不是自身的后继状态，而是进入对手的新状态，只有当自身再次行动时，此时的状态才是后继状态：S⁰_blue → A⁰_blue → S⁰_red → A⁰_red → S¹_blue  → A¹_blue  → S¹_red →  A¹_red  → S²_blue → …，Q表中的状态数是4520，大于这个数字说明代码一定是哪里写错了）
2. 构建一个 ε-greedy 策略函数 epsilon_greedy(env)，并区分蓝/红方，红方（陪练）动作时，把当前状态翻转。
3. 构建一个往Q表格新增状态的函数 addNewState(env), 并区分蓝/红方，红方调用时，把当前状态翻转。　　
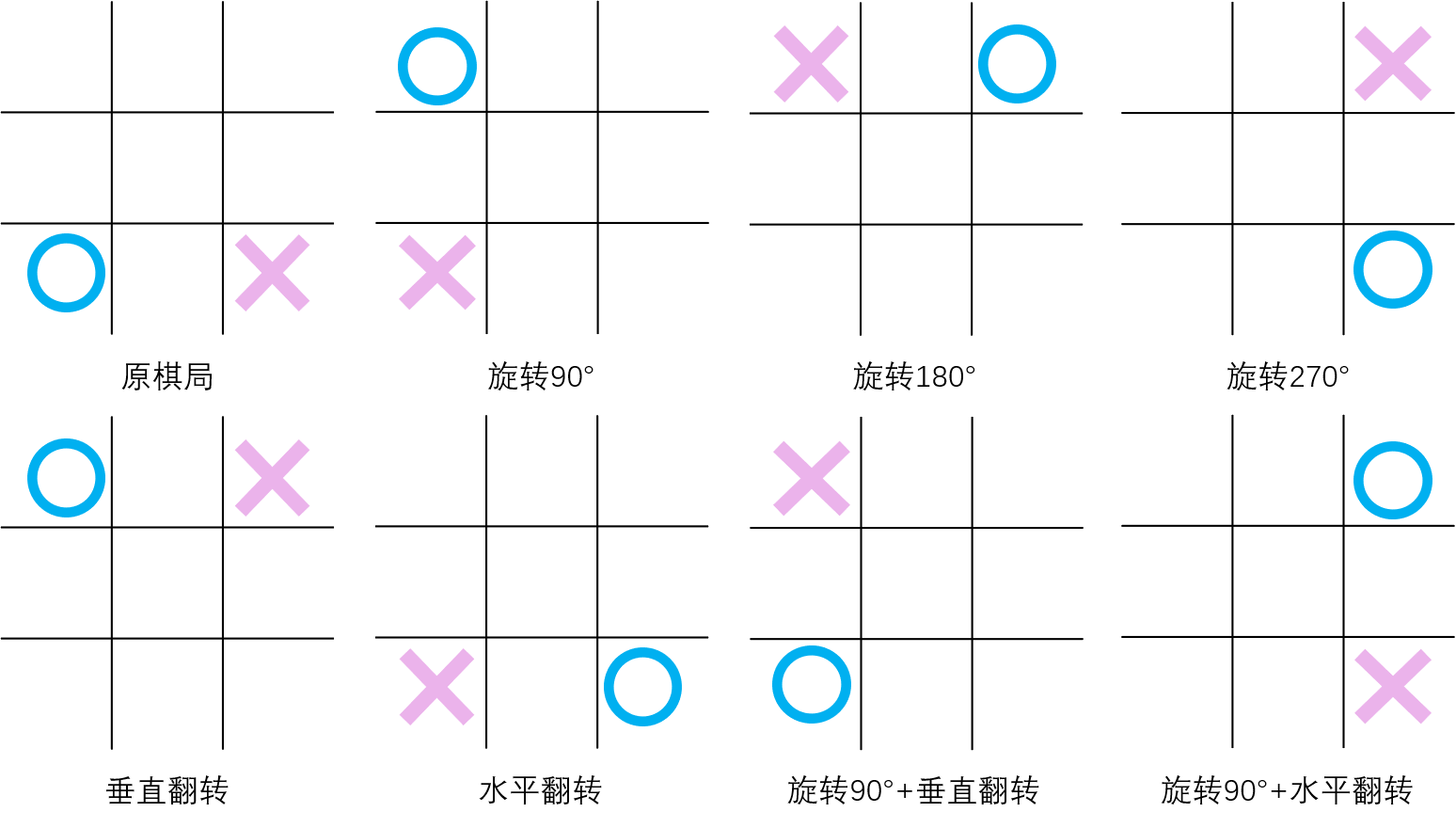
4. 构建一个更新Q表格状态价值的函数 updateQtable(env)，可以选择锁定蓝方视角：蓝方行动前调用，也可以选择蓝方和红方视角下都调用（红方调用时需要翻转状态），可以想到，这样的双向调用在相同轮次内更新的状态更多。另一个加快更新的方法是考虑等价的棋局，翻转或旋转运动可以创造等价的7个棋局（见下图），分别是：旋转90°，旋转180°，旋转270° ，垂直翻转，水平翻转，旋转90°+垂直翻转，旋转90°+水平翻转。双向更新+等价棋局同步更新，这样我们就能在一轮对局中更新 2×8=16 个Q值，大大提高了更新速度。　　

秉着“先跑通，再优化”的信条，先实现蓝红两方的双向更新，等价棋局的更新下次一定。整体代码如下：

import gym
import random
import time

# 查看所有已注册的环境
# from gym import envs
# print(envs.registry.all()) 

def str2tuple(string): # Input: '(1,1)'
    string2list = list(string)
    return ( int(string2list[1]), int(string2list[4]) ) # Output: (1,1)

class Game():
    def __init__(self, env):
        self.INTERVAL = 0 # 行动间隔
        self.RENDER = False # 是否显示游戏过程
        self.first = 'blue' if random.random() > 0.5 else 'red' # 随机先后手
        self.currentMove = self.first
        self.env = env
        self.agent = Agent()

    def switchMove(self): # 切换行动玩家
        move = self.currentMove
        if move == 'blue': self.currentMove = 'red'
        elif move == 'red': self.currentMove = 'blue'

    def newGame(self): # 新建游戏
        self.first = 'blue' if random.random() > 0.5 else 'red'
        self.currentMove = self.first
        self.env.reset()
        self.agent.reset()

    def run(self): # 玩一局游戏
        self.env.reset() # 在第一次step前要先重置环境，不然会报错
        while True:
            print(f'--currentMove: {self.currentMove}--')
            self.agent.updateQtable(self.env, self.currentMove, False)

            if self.currentMove == 'blue':
                self.agent.lastState_blue = self.env.state.copy()
            elif self.currentMove == 'red':
                self.agent.lastState_red = self.agent.overTurn(self.env.state) # 红方视角需将状态翻转

            action = self.agent.epsilon_greedy(self.env, self.currentMove)
            if self.currentMove == 'blue':
                self.agent.lastAction_blue = action['pos']
            elif self.currentMove == 'red':
                self.agent.lastAction_red = action['pos']

            state, reward, done, info = self.env.step(action)
            if self.currentMove == 'blue':
                self.agent.lastReward_blue = reward
            elif self.currentMove == 'red':
                self.agent.lastReward_red = -1 * reward

            if done: self.agent.updateQtable(self.env, self.currentMove, True)

            if self.RENDER: self.env.render()
            self.switchMove()
            time.sleep(self.INTERVAL)
            if done:
                self.newGame()
                if self.RENDER: self.env.render()
                time.sleep(self.INTERVAL)
                break

class Agent():
    def __init__(self):
        self.Q_table = {}
        self.EPSILON = 0.05
        self.ALPHA = 0.5
        self.GAMMA = 1 # 折扣因子
        self.lastState_blue = None
        self.lastAction_blue = None
        self.lastReward_blue = None
        self.lastState_red = None
        self.lastAction_red = None
        self.lastReward_red = None

    def reset(self):
        self.lastState_blue = None
        self.lastAction_blue = None
        self.lastReward_blue = None
        self.lastState_red = None
        self.lastAction_red = None
        self.lastReward_red = None

    def getEmptyPos(self, env_): # 返回空位的坐标
        action_space = []
        for i, row in enumerate(env_.state):
            for j, one in enumerate(row):
                if one == 0: action_space.append((i,j))
        return action_space

    def randomAction(self, env_, mark): # 随机选择空格动作
        actions = self.getEmptyPos(env_)
        action_pos = random.choice(actions)
        action = {'mark':mark, 'pos':action_pos}
        return action

    def overTurn(self, state): # 翻转状态
        state_ = state.copy()
        for i, row in enumerate(state_):
            for j, one in enumerate(row):
                if one != 0: state_[i][j] *= -1
        return state_

    def addNewState(self, env_, currentMove): # 若当前状态不在Q表中，则新增状态
         state = env_.state if currentMove == 'blue' else self.overTurn(env_.state) # 如果是红方行动则翻转状态
         if str(state) not in self.Q_table:
             self.Q_table[str(state)] = {}
             actions = self.getEmptyPos(env_)
             for action in actions:
                 self.Q_table[str(state)][str(action)] = 0

    def epsilon_greedy(self, env_, currentMove): # ε-贪心策略
        state = env_.state if currentMove == 'blue' else self.overTurn(env_.state) # 如果是红方行动则翻转状态
        Q_Sa = self.Q_table[str(state)]
        maxAction, maxValue, otherAction = [], -100, []
        for one in Q_Sa:
            if Q_Sa[one] > maxValue:
                maxValue = Q_Sa[one]
        for one in Q_Sa:
            if Q_Sa[one] == maxValue:
                maxAction.append(str2tuple(one))
            else:
                otherAction.append(str2tuple(one))

        try:
            action_pos = random.choice(maxAction) if random.random() > self.EPSILON else random.choice(otherAction)
        except: # 处理从空的otherAction中取值的情况
            action_pos = random.choice(maxAction)
        action = {'mark':currentMove, 'pos':action_pos}
        return action

    def updateQtable(self, env_, currentMove, done_):

        judge = (currentMove == 'blue' and self.lastState_blue is None) or \
                (currentMove == 'red' and self.lastState_red is None)
        if judge: # 边界情况1：若agent无上一状态，说明是游戏中首次动作，那么只需要新增状态就好 无需更新Q值
            self.addNewState(env_, currentMove)
            return

        if done_: # 边界情况2：若当前状态S_是终止状态，则无需把S_添加至Q表格中，并直接令maxQ_S_a = 0
            S = self.lastState_blue  if currentMove == 'blue' else self.lastState_red
            a = self.lastAction_blue if currentMove == 'blue' else self.lastAction_red
            R = self.lastReward_blue if currentMove == 'blue' else self.lastReward_red
            print('lastState S:\n', S)
            print('lastAction a: ', a)
            print('lastReward R: ', R)
            maxQ_S_a = 0
            self.Q_table[str(S)][str(a)] = (1 - self.ALPHA) * self.Q_table[str(S)][str(a)] \
                                            + self.ALPHA * (R + self.GAMMA * maxQ_S_a)
            print('Q(S,a) = ', self.Q_table[str(S)][str(a)])
            return

        # 其他情况下：Q表无当前状态则新增状态，否则直接更新Q值
        self.addNewState(env_, currentMove)
        S_ = env_.state if currentMove == 'blue' else self.overTurn(env_.state)
        S = self.lastState_blue  if currentMove == 'blue' else self.lastState_red
        a = self.lastAction_blue if currentMove == 'blue' else self.lastAction_red
        R = self.lastReward_blue if currentMove == 'blue' else self.lastReward_red
        Q_S_a = self.Q_table[str(S_)]
        maxQ_S_a = -100
        for one in Q_S_a:
            if Q_S_a[one] > maxQ_S_a:
                maxQ_S_a = Q_S_a[one]
        print('lastState S:\n', S)
        print('State S_:\n', S_)
        print('lastAction a: ', a)
        print('lastReward R: ', R)
        self.Q_table[str(S)][str(a)] = (1 - self.ALPHA) * self.Q_table[str(S)][str(a)] \
                                        + self.ALPHA * (R + self.GAMMA * maxQ_S_a)
        print('Q(S,a) = ', self.Q_table[str(S)][str(a)])
        print('\n')

env = gym.make('TicTacToeEnv-v0')
game = Game(env)
for i in range(100000):
    print('episode', i)
    game.run()
Q_table = game.agent.Q_table

测试

先跑个10万局游戏，看看大体的趋势对不对。

项目1：Q表格的状态数

比4520要小——这是可以理解的，因为agent有1- ε的大概率选择Q值高的动作，仅有 ε会尝试别的动作。要访问到余下的状态，可以加大 ε 让agent多尝试，或是干脆让陪练随机动作，或是设置等价棋局同步更新以提高训练速度。

项目2：查看初始状态

每个动作的Q值应该都差不多，而且应该呈现出对称性

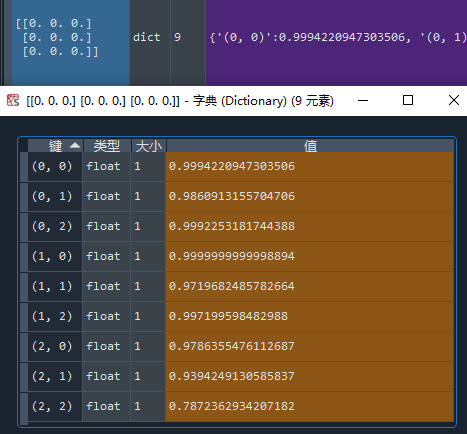
与预测不完全一致，毕竟（0，0）与（2，2）动作后是等价局面，二者Q值应该接近，但也可以接受，毕竟没有进行等价棋局的同步更新。

项目3：查看早期状态

早期状态应该能显示出某些动作具有相对低的Q值——“走这一步你大概就输了”。

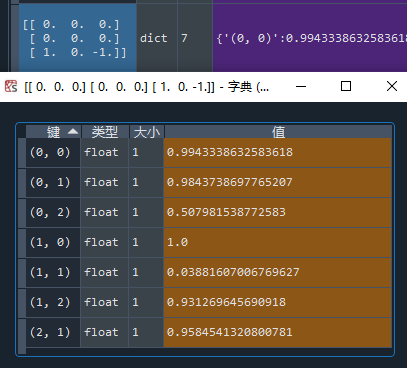
因为有学习率的存在，Q值只会无限接近1，这里显示成了1，说明无限接近到float也显示不出来了，（1，0）是必胜的一步，而选择（1，1）约等于自杀。

项目4：查看中后期的状态

中后期的状态应该能显示出某些动作是必赢 / 必输的。

“走哪里都输”：

“走这一步，必赢”：

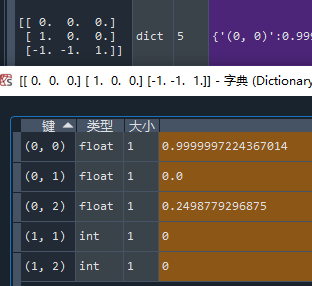
走（0，0）确实是必赢的，你看出来了吗？

小结

测试过后，大体的趋势没有问题，但我在翻查Q表格的时候发现，其实很多状态都没有更新，Q表格也没有覆盖所有合法状态。这些问题，就留到下一节来解决吧！

说一说踩的坑

• 本以为翻转状态可以直接优雅地 state =  -1 * state，但转换成字符判定时却遇到了问题，因为numpy.array的元素 0 * -1 = - 0，转换成字符串后 '0' 不等于 '-0'！解决方法：只更改 1 和 -1。
• 深拷贝与浅拷贝的问题，self.agent.lastState_blue = self.env.state，不是直接赋值，而是赋予了 self.env.state 的引用，所以 self.agent.lastState_blue 的值是变化的，然后导致一系列的错误。解决方法：self.agent.lastState_blue = self.env.state.copy()。
• 有两个边界情况要注意，一是首次动作时没有上一状态；二是动作后若游戏结束，要直接更新Q值。