【数组】Subsets

题目：

Given a set of distinct integers, nums, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If nums = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

思路：

方法一：

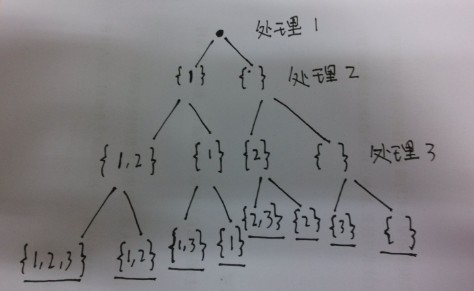
求集合的所有子集问题。题目要求子集中元素非递减序排列，因此我们先要对原来的集合进行排序。原集合中每一个元素在子集中有两种状态：要么存在、要么不存在。这样构造子集的过程中每个元素就有两种选择方法：选择、不选择，因此可以构造一颗二叉树，例如对于例子中给的集合[1,2,3]，构造的二叉树如下（左子树表示选择该层处理的元素，右子树不选择），最后得到的叶子节点就是子集：

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function(nums) {
            var res=[];
            nums.sort(function(a,b){return a-b;});
 
            var tempRes=[];
            dfs(nums,0,tempRes);
            return res;
 
            function dfs(nums,iEnd,tempRes){
                var temp=[];
                for(var i=0;i<tempRes.length;i++){
                    temp[i]=tempRes[i];
                }
 
                if(iEnd==nums.length){
                    res.push(temp);
                    return;
                }
                //选择
                temp.push(nums[iEnd]);
                dfs(nums,iEnd+1,temp);
                //不选
                temp.pop();
                dfs(nums,iEnd+1,temp);
            }
        };

方法二：

从上面的二叉树可以观察到，当前层的集合 = 上一层的集合 + 上一层的集合加入当前层处理的元素得到的所有集合（其中树根是空集），因此可以从第二层开始（第一层是空集合）迭代地求最后一层的所有集合（即叶子节点）

方法三：

可以根据二进制的思想，比如对于3个元素的集合，000表示一个元素都不选择，001表示选择第一个元素，101表示选择第一个和第三个元素...。因此如果集合大小为n，我们只需要让一个整数从0逐渐增加到2^n-1, 每个整数的二进制形式可以表示一个集合。如果用整数的二进制表示集合，这个算法有个限制，最大能表示集合元素的个数为64（unsigned long long）。如果使用bitmap，然后模拟二进制的加1操作，则对集合大小就没有限制。刚好这一题集合的大小不超过64